решите уравнение sinx+cosx=1-sin2x
Аноним:
может быть sinx - cosx = 1-sin2x??
^ тоже самое :D в квадрате может?)))
а не минус же
нет так будет слишком просто :) У меня после получаса это, кажется к биквадратному уравнению сводится
когда все просто-это же хорошо :DD
Ответы
Ответ дал:
0
как-то так
 (1)
(1)

обозначим
u=sin(x)
тогда

уравнение примет вид

возводим обе части равенства в квадрат (Вот тут влез лишний корень u=-1)

 (ЖЖ)
(ЖЖ)
 (Ж)
(Ж)
сокращаем на при этом
при этом  ≠0 проверить
≠0 проверить

снова обе части в квадрат


Проверьте Нигде не хомутнул.
Ну дальше уже проще
обозначим
-4v^2+4v-9=0
Да это уравнение вещественных корней не имеет, так как дискриминант <0, как справедливо заметили коллеги.
НО
Мы делили на могли потерять решение
могли потерять решение
при
тогда (Ж) обращается в верное равенство.
Значит, надо рассмотреть уравнение
при
Ну а,это решение уже имеет корни


u=sin(x)=-1 придется отбросить, ибо такое значение не удовлетворяет исходному уравнению (1)


где к целые числа
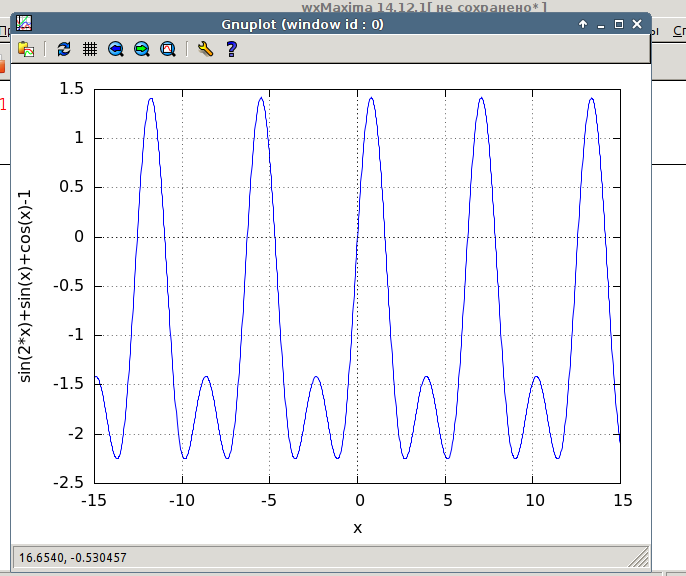
Да судя по рисунку мы еще потеряли корни.
Да там где (ЖЖ) мы делили (сокращали на 2u)
u=0 тоже обращает (ЖЖ) в верное равенство
Тогда

И еще один набор корней

где n целое n=0, +-1, +-2, +-3 и тд
Блин, а судя по картинке, остаются только,

где n целое n=0, +-1, +-2, +-3 и тд
обозначим
u=sin(x)
тогда
уравнение примет вид
возводим обе части равенства в квадрат (Вот тут влез лишний корень u=-1)
сокращаем на
снова обе части в квадрат
Проверьте Нигде не хомутнул.
Ну дальше уже проще
обозначим
-4v^2+4v-9=0
Да это уравнение вещественных корней не имеет, так как дискриминант <0, как справедливо заметили коллеги.
НО
Мы делили на
при
тогда (Ж) обращается в верное равенство.
Значит, надо рассмотреть уравнение
при
Ну а,это решение уже имеет корни
u=sin(x)=-1 придется отбросить, ибо такое значение не удовлетворяет исходному уравнению (1)
где к целые числа
Да судя по рисунку мы еще потеряли корни.
Да там где (ЖЖ) мы делили (сокращали на 2u)
u=0 тоже обращает (ЖЖ) в верное равенство
Тогда
И еще один набор корней
где n целое n=0, +-1, +-2, +-3 и тд
Блин, а судя по картинке, остаются только,
где n целое n=0, +-1, +-2, +-3 и тд
Приложения:
а так
Вообще да дискриминант меньше 0
Печально, но не комплексным же числам переходить
Если через них, то решение есть в любом случае
Да должны быть корни исходного уравнения, если график построить видно
черт, хоть численно методом вилки решай
-1 не будет верным) вот поставьте
и у вас x=0 похоже потерян
Да если в уравнение подставить sin(x)=-1 не получается. Но вот как он примазался.
это просто офигеть)))))))
Ответ дал:
1
**********************************************
Приложения:

да я из картинки уже вижу, а как его отбраковали?
Как так сразу решили, что он посторонний?
и у вас x=0 похоже потерян
Да если в уравнение подставить sin(x)=-1 не получается. Но вот как он примазался.
Бедняга вопрошающий! Ему придется как-то лепить решение из двух кошмариков
Тут Потерян набор корней x=pi*n
Похожие вопросы
1 год назад
2 года назад
6 лет назад