Предмет: Алгебра
Автор: vampirchikiris
Вопрос задан 2 года назад

Найти наименьшее и наибольшее значение функции y=f(x) на отрезке [a;b]
y=3x/(x^2+1) ; [0;5]

Приложения:

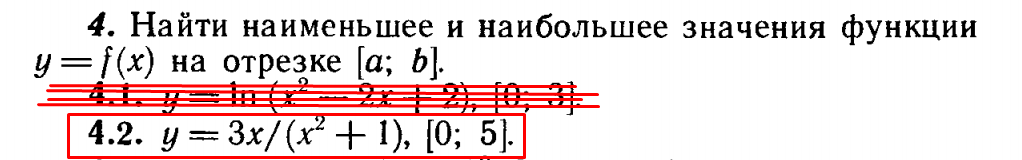
Ответы

Ответ дал: kilzer

Посмотрим на производную этой функции.
$f'(x) = \frac{3}{x^2+1} - \frac{3x*2x}{(x^2+1)^2} = 3* \frac{1-x^2}{(x^2+1)^2}$
Посмотрим на то, какие знаки эта производная принимает. Знаменатель всегда положителен. Точки смены знака две: $1$ и $-1$ . При чём при больших $x$ $f'(x)$ отрицательно. Таким образом, производная отрицательна на отрезках $(-\infty; -1]$ и $[1; \infty)$ , а положительна на отрезке $[-1; 1]$ . Функция возрастает в точке тогда и только тогда, когда производная в этой точке положительна, а убывает тогда и только тогда, когда производная отрицательна. Отсюда видно, что максимум на отрезке функция достигнет в точке $1$ , наибольшее значение, таким образом, равно $1.5$ , а минимум будет в одном из концов отрезка -- либо в $0$ (значение -- $0$ ), либо в $5$ (значение -- $\frac{15}{26}$ ). Мы видим, что в 0 значение меньше. Поэтому минимум функции на этом отрезке -- 0. Максимум -- 1.5