Предмет: Математика
Автор: lapan12
Вопрос задан 2 года назад

помогите решить предел

Приложения:

Ответы

Ответ дал: Exponena

Ладно. Кто как его брал не знаю. Поясню, как получилось у меня.
$\lim_{x \to \infty} \frac{2^{ \sqrt{x+1}- \sqrt{x} } }{x+1}$ (1)
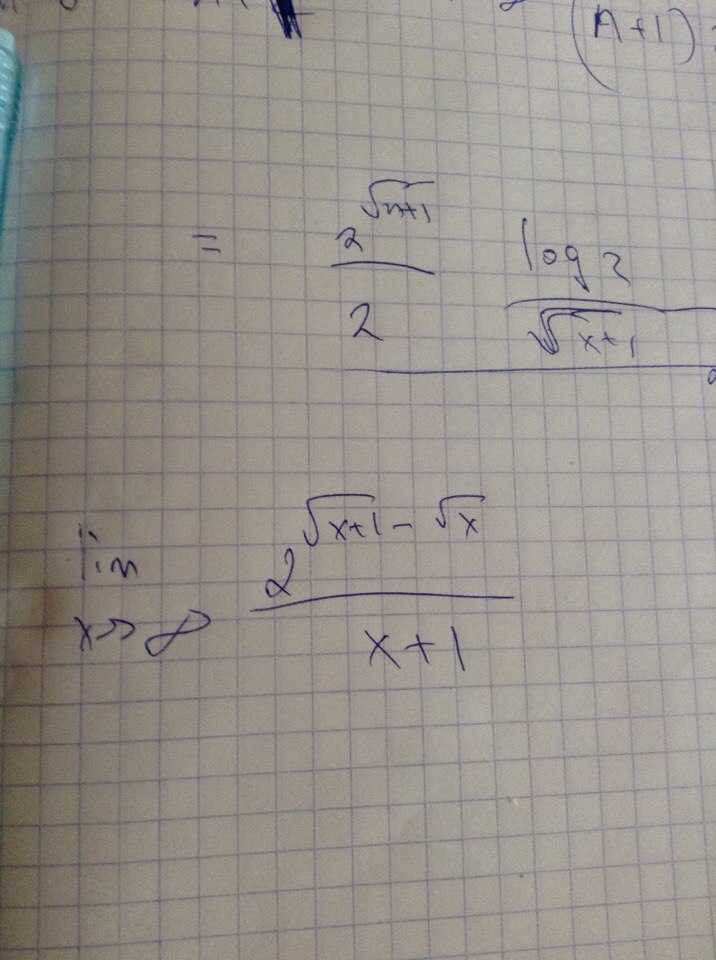
Глядя на этот предел кажется мне, что предел числителя будет конечен.
Попробуем это подтвердить (опровергнуть.) Прежде всего перейдем к пределу в показателе. Т.е Если в выражении
$\lim_{x \to x_{0}} 2^{f(x) }$ , a не зависит от x и
существует конечный предел функции f(x) в точке x0, то верно:
$\lim_{x \to x_{0}} a^{f(x) }= a^{\lim_{x \to x_{0}} f(x) }$

Хорошо, значит нам нужно найти предел:
$\lim_{x \to \infty} ( \sqrt{x+1}- \sqrt{x} )$ (2)

$\lim_{x \to \infty} ( \sqrt{x+1}- \sqrt{x} )=\lim_{x \to \infty} (\sqrt{x}( \sqrt{1+ \frac{1}{x} }- 1 ))$ (3)
Введем новую переменную
$t= \sqrt{x}$
Тогда если x⇒∞ то и t⇒∞, а наш предел (3) принимает вид:
$\lim_{x \to \infty} (\sqrt{x}( \sqrt{1+ \frac{1}{x} }- 1 ))=\lim_{t \to \infty} (t( \sqrt{1+ \frac{1}{t^2} }- 1 ))$ (4)
Смотрим далее соотношение:
$\sqrt{1+ \frac{1}{t^2}$ на основании формулы бинома Ньютона для дробной степени:
$(1+ \alpha )^{1/n}=1+ \frac{ \alpha }{n} +o( \alpha )$ где $\alpha \ \textless \ 1$ (а у нас при $t \to \infty$ $\frac{1}{t^2} \to 0$ )
заменяем эквивалентным выражением
$\sqrt{1+ \frac{1}{t^2}}=1+ \frac{1}{2t^2}$

Тогда (4) преобразуется к виду:
$\lim_{t \to \infty} (t( \sqrt{1+ \frac{1}{t^2} }- 1 ))=\lim_{t \to \infty} (t*( 1+ \frac{1}{2t^2}+o( \frac{1}{t^2} )- 1 ))=$
$\lim_{t \to \infty} (t*( 1+ \frac{1}{2t^2}+o( \frac{1}{t^2} )- 1 ))=\lim_{t \to \infty} (t*( \frac{1}{2t^2}))=$ $=\lim_{t \to \infty} ( \frac{t}{2t^2})=\lim_{t \to \infty} ( \frac{1}{2t})=0$
Т.е предел (4) (показатель степени) стремится к 0. Значит числитель дроби стремится к 1. А предел знаменателя ∞. т.е. получаем предел вида:
$\frac{1}{\infty}$ , ну а это 0.
Таким образом исходный предел (1) равен нулю:
$\lim_{x \to \infty} \frac{2^{ \sqrt{x+1}- \sqrt{x} } }{x+1} =0$

Похожие вопросы

История

1 год назад

Задание 1. Заполните схему социального устройства казахского ханства

Русский язык

1 год назад

Заполните пропуски подходящими словами из списка: можно, нельзя, иноязычных, русских. Гласные после приставок, оканчивающихся на согласные, проверить ударением. Их правописание зависит от

Другие предметы

1 год назад

1.Какие качества характера вырабатываются в походе? 2.Как поход влияет на взаимоотношения в колективе? 3.Что самое тоудное,а что самое интересное в походе?

Английский язык

1 год назад