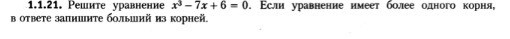Ответы
Ответ дал:
0
х³-7х+6 = 0
х³-х-6х+6 = 0
х(х²-1)-6(х-1) = 0
х(х+1)(х-1)-6(х-1) = 0
(х-1)(х(х+1)-6) = 0
(х-1)(х²+х-6) = 0
х²+х-6 = 0 х-1 = 0
х₁+х₂ = -1 х = 1
х₁*х₂ = -6
х₁ = -3
х₂ = 2
Ответ: наибольший корень х = 2
х³-х-6х+6 = 0
х(х²-1)-6(х-1) = 0
х(х+1)(х-1)-6(х-1) = 0
(х-1)(х(х+1)-6) = 0
(х-1)(х²+х-6) = 0
х²+х-6 = 0 х-1 = 0
х₁+х₂ = -1 х = 1
х₁*х₂ = -6
х₁ = -3
х₂ = 2
Ответ: наибольший корень х = 2
Ответ дал:
0
x³ -7x+6=0
Проверим является ли х=1 - корнем уравнения?
х=1 1³-7*1+6=0
-6+6=0
0=0
х=1 - корень уравнения.
Значит исходное уравнение можно разложить на множители, один из которых равен (х-1). Разделим
_ х³ -7х+6 | x-1
_ x³-x² x²+x-6
_ x²-7x
_ x²-x
_ -6x+6
-6x+6
0
В итоге:
x³-7x+6=(x-1)(x²+x-6)
(x-1)(x²+x-6)=0
x-1=0 x²+x-6=0
x=1 D=1+4*6=25
x₁=-1-5=-3
2
x₂=-1+5=2
2
x=-3; х=1; х=2 - корни уравнения.
х=2 - наибольший корень.
Ответ: 2.
Проверим является ли х=1 - корнем уравнения?
х=1 1³-7*1+6=0
-6+6=0
0=0
х=1 - корень уравнения.
Значит исходное уравнение можно разложить на множители, один из которых равен (х-1). Разделим
_ х³ -7х+6 | x-1
_ x³-x² x²+x-6
_ x²-7x
_ x²-x
_ -6x+6
-6x+6
0
В итоге:
x³-7x+6=(x-1)(x²+x-6)
(x-1)(x²+x-6)=0
x-1=0 x²+x-6=0
x=1 D=1+4*6=25
x₁=-1-5=-3
2
x₂=-1+5=2
2
x=-3; х=1; х=2 - корни уравнения.
х=2 - наибольший корень.
Ответ: 2.
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
6 лет назад
6 лет назад
8 лет назад