Предмет: Алгебра
Автор: khmyzova97Gosha
Вопрос задан 2 года назад

< >

Помогите,пожалуйста!
Нужно решить системой уравнений

Приложения:

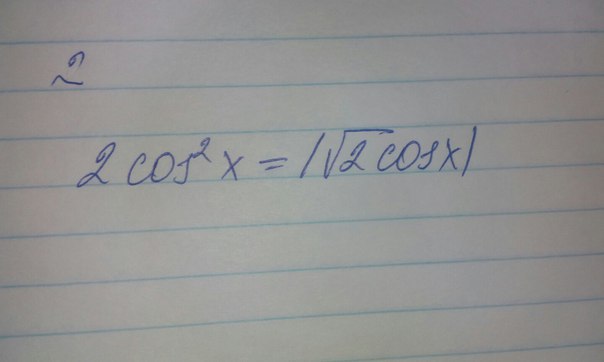
HenryDukart: Системой или совокупностью?

khmyzova97Gosha: совокупность систем

Ответы

Ответ дал: mukus13

5

$2cos^2x=| \sqrt{2} cosx |$
ОДЗ: $2cos^2x \geq 0$
$2cos^2x= \sqrt{2} cosx$ или $2cos^2x=- \sqrt{2} cosx$
$2cos^2x- \sqrt{2} cosx=0$ или $2cos^2x+ \sqrt{2} cosx=0$
$cosx(2cosx- \sqrt{2} )=0$ или $cosx(2cosx+ \sqrt{2} )=0$
$cosx=0$ или $2cosx- \sqrt{2} =0$ или $2cosx+ \sqrt{2} =0$
$x= \frac{ \pi }{2} + \pi k,$ k∈Z или $cosx= \frac{ \sqrt{2} }{2}$ или $cosx=- \frac{ \sqrt{2} }{2}$
$x= \frac{ \pi }{2} + \pi k,$ k∈Z или $x=$ ± $\frac{ \pi }{4} +2 \pi n,$ n∈z или $x=$ ± $\frac{3 \pi }{4} +2 \pi m,$ m∈Z

mukus13: уравнение равносильно совокупности 2 условий

mukus13: вместо или можно ставить квадратную скобку - это и есть совокупность

khmyzova97Gosha: спасибо, я поняла. Очень благодарна вам

Ответ дал: Аноним

1

Смотреть во вложении

Приложения:

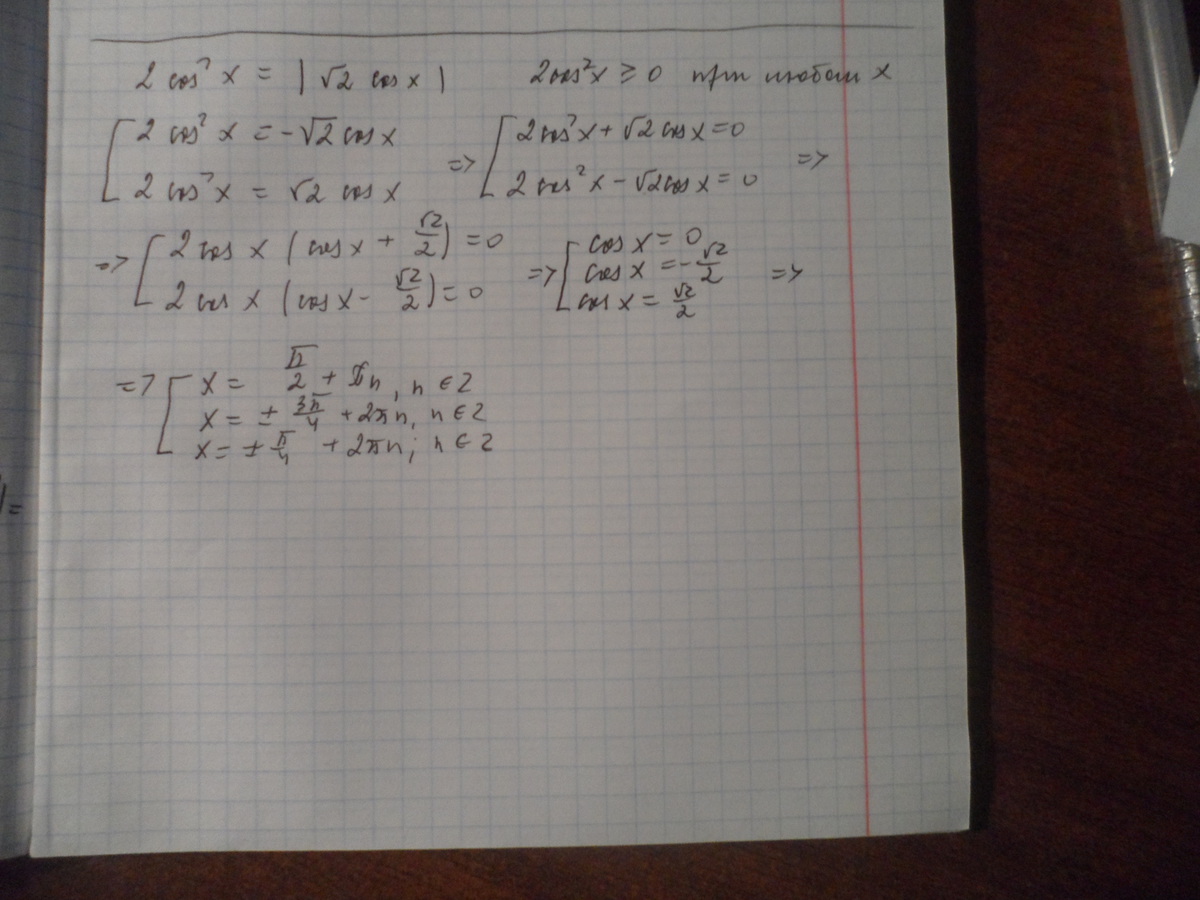
Похожие вопросы

Математика

1 год назад

найдите значение выражения cos^2 45+sin^2 74+cos^2 74

Русский язык

1 год назад

А Упражнение 329. Спишите текст, вставляя, где нужно, пропу- щенные буквы. Приведите примеры на правописание безударной гласной в корне, непроизносимой согласной в корне, правописание гласных

Другие предметы

1 год назад

с помощью учебника напиши, чем отличаются права от обязанностей. сравним свой ответ с ответами одноклассников

Окружающий мир

1 год назад

Закончи предложения свекла сладкая а лук

Литература

6 лет назад

характеристика Онєгіна як тип зайвої людини

Русский язык

6 лет назад

6 класс алые паруса. помогите пожалуйста, дам 50 баллов)

Алгебра

8 лет назад

кого вы любите больше своей жизни???

Геометрия

8 лет назад

начертите окружность с центром в точке О и радиусом r=3,5 см.Проведите диаметр и радиусы разноцветными карандашами с картинкой с разноцветными карандашами плз