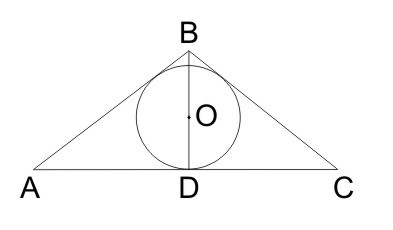
В равнобедренном треугольнике центр вписанного круга делит высоту в отношении 12:5, а боковая сторона равна 60 м. Найдите основание.
(Источник: Крамор В.С. Повторяем и систематизируем школьный курс геометрии, М., 1992, с. 96)
Приложения:
Ответы
Ответ дал:
31
АВ=ВС=60
ВО/ДО=12/5
Центр вписанной в треугольник окружности есть точка пересечения его биссектрис. Значит АО - это биссектриса.
По свойству биссектрисы треугольника:
АВ/ВО=АД/ДО
ВО/ДО=АВ/АД
12/5=АВ/АД
АД=5АВ/12=5*60/12=25
В равнобедренном треугольнике высота - это и медиана АД=ДС.
Значит АС=2*25=50
ВО/ДО=12/5
Центр вписанной в треугольник окружности есть точка пересечения его биссектрис. Значит АО - это биссектриса.
По свойству биссектрисы треугольника:
АВ/ВО=АД/ДО
ВО/ДО=АВ/АД
12/5=АВ/АД
АД=5АВ/12=5*60/12=25
В равнобедренном треугольнике высота - это и медиана АД=ДС.
Значит АС=2*25=50
Аноним:
Спасибо! Совсем я это свойство биссектрис упустил из виду...
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
6 лет назад
8 лет назад