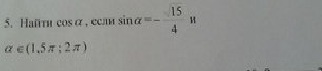Ответы
Ответ дал:
1
Вспомним основное тригонометрической тождество 
Так как , то есть угол находится в IV (4) четверти, то косинус будет положительным
, то есть угол находится в IV (4) четверти, то косинус будет положительным

Так как
Ответ дал:
0
Похожие вопросы
1 год назад
2 года назад
2 года назад
6 лет назад
6 лет назад
8 лет назад
8 лет назад