В прямоугольном треугольнике PQR с прямым углом Q проведена высота QL.Докажите,что PQ2=PLxPR
МОЖНО ТОЛЬКО РИСУНОК ЧЕРТЕЖ И ВСЕ РЕШЕНИЯ НЕ НАДО!!!!!!
cos20093:
Чего тут рисовать - прямоугольный треугольник и высота к гипотенузе. Всего 4 линии. Высота делит треугольник на 2, и оба они подобны исходному - потому что углы общие есть. Ну и между собой они тоже тогда подобны. Из этого подобия можно составить пропорции. Ну, типа x/h = h/y;... x = PL; y = RL; h = PQ; в условии равенство записано неверно, такого соотношения нет. PQ^2 = PL*LR;
Мда, надо было чертеж нарисовать :) есть такое соотношение :) это QL^2 = PL*RL; а тут из подобия треугольников PQR и PQL получается PL/PQ = PQ/PR; PQ^2 = PL*PR; то есть оба соотношения доказываются одинаково.
Ответы
Ответ дал:
0
Смотреть во вложении
Приложения:
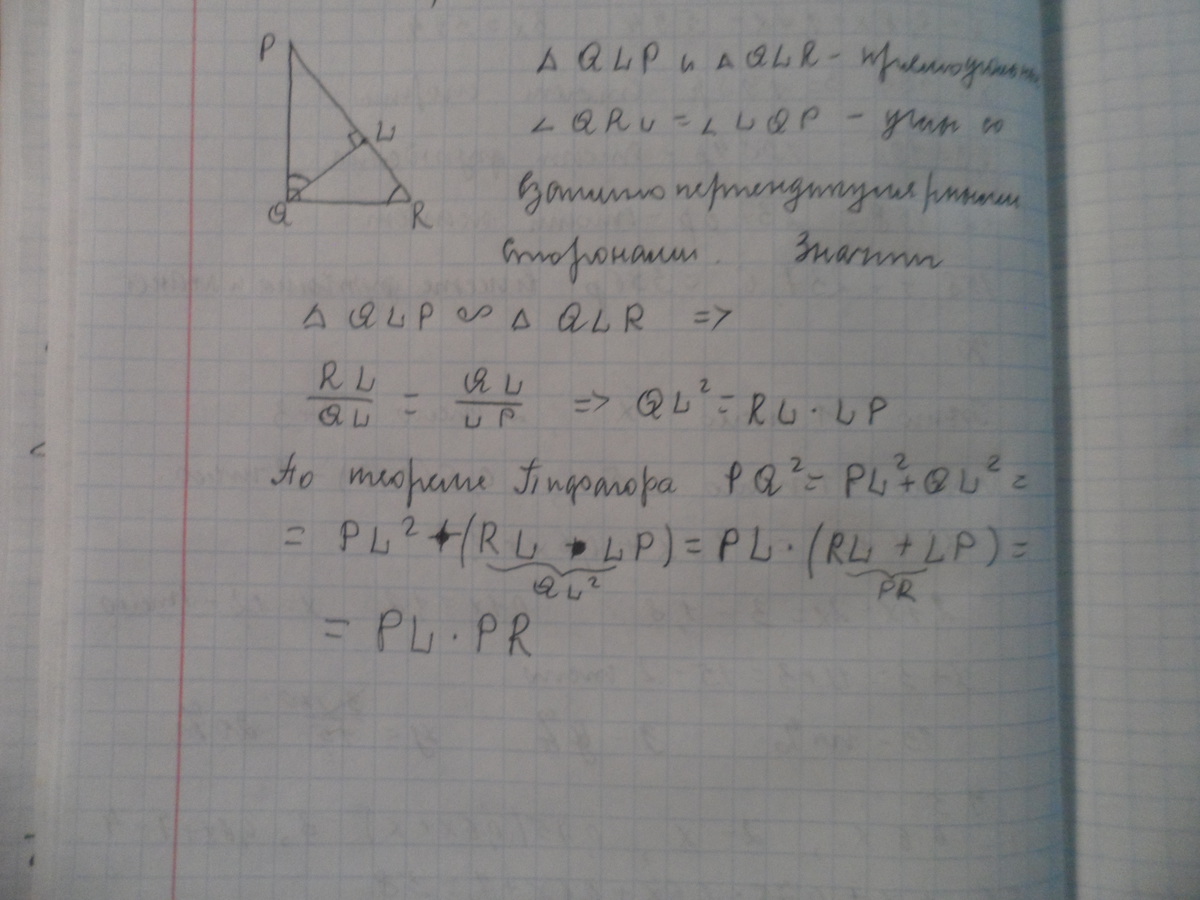
Ответ дал:
0
ΔPLQ под ΔPQR (< P-общий острый угол)
PQ/PR =PL/PQ ⇒PQ² =PL*PR.
------------------- или ----------------
cos<P = PQ/PR = PL/PQ .
* * * Из ΔPQR: cos<P = PQ/PR ; Из ΔPLQ : cos<P = PL/PQ . * * *
Похожие вопросы
1 год назад
1 год назад
1 год назад
6 лет назад
6 лет назад
8 лет назад
8 лет назад