Помогите пожалуйста - Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют условиям
Далее система
x^2+y^2 ≤ 4(x+y-1)
y≤|x-2| (здесь модуль)

и найдите площадь получившейся фигуры

первый график
х²+у²≤4(х+у-1)
преобразуем, получим
(х-2)²+(у-2)²≤4
множество точек внутри окружности с центром (2;2) и радиусом 2 и сама окружность
второй график
у≤|x-2|
множество точек ниже графика у=|x-2| и сам график
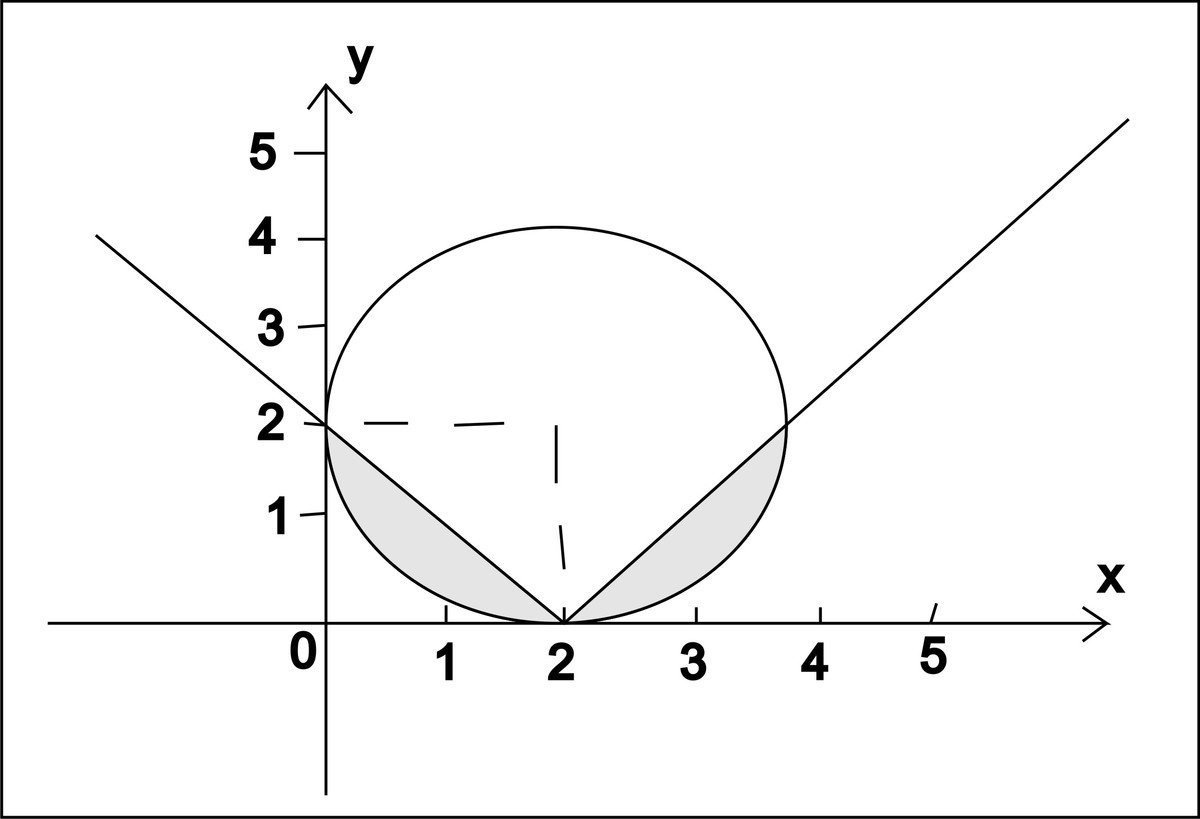
на рисунке показана область пересечения данных множеств
это два одинаковых сегмента
площадь одного семента S=(R²/2)·(α-sinα)=(4/2)·((π/2)-1)=π-2
площадь получившейся фигуры равна площади двух секторов S=2π-4
Ответ 2π-4