Высота приямоугольного треугольника, опущенная на гипотенузу 8 см, а один из катетов 17 см.
Найти длину гипотенузы.
Ответы
Ответ дал:
1
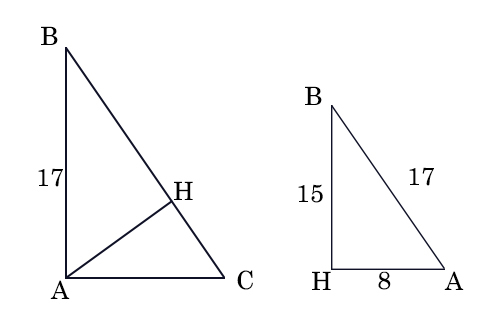
ΔАВС: ВС- гипотенуза, АН=8(высота)
ВН²=225, ВН=15
ΔАВС и ΔНВА - похожие( 2 угла и сторона)
АВ/ВН=ВС/ВА
17/15=ВС/17
ВС=289/15
Ответ: 289/15
ВН²=225, ВН=15
ΔАВС и ΔНВА - похожие( 2 угла и сторона)
АВ/ВН=ВС/ВА
17/15=ВС/17
ВС=289/15
Ответ: 289/15
Приложения:
артем007164:
Это точно.
... длина 289/15?
O.o
это дробь. цифра не круглая, но выходит именно так
вот прикрепила и рисунок, дабы и самой убедится )
Ответ дал:
0
Вариант решения.
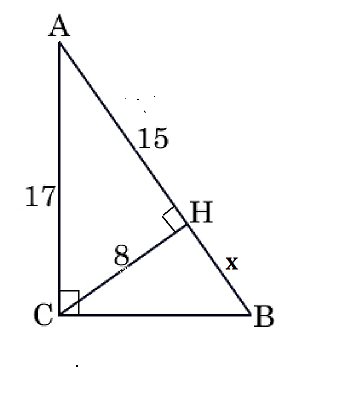
Из прямоугольного треугольника АСН найдем по т. Пифагора катет АН. ( отношение сторон из троек Пифагора 15:8:17, можно без подсчетов узнать АН. Он равен 15 см.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
Следовательно,
СН²=АН*ВН
64=15*ВН
ВН=64/15
АВ=АН+НВ=(15*15+64)/15=289/15
Из прямоугольного треугольника АСН найдем по т. Пифагора катет АН. ( отношение сторон из троек Пифагора 15:8:17, можно без подсчетов узнать АН. Он равен 15 см.
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой;
Следовательно,
СН²=АН*ВН
64=15*ВН
ВН=64/15
АВ=АН+НВ=(15*15+64)/15=289/15
Приложения:
Похожие вопросы
1 год назад
1 год назад
1 год назад
1 год назад
6 лет назад
8 лет назад