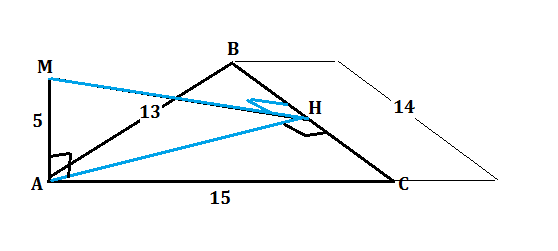
МА - перпендикуляр к плоскости треугольника АВС. Найти расстояние от точки М к прямой ВС, если АВ = 13см, ВС = 14см, АС = 15см, АМ=5см. Напишите, пожалуйста, решение. Заранее спасибо)

Расстояние от точки до прямой - отрезок, перпендикулярный к этой прямой, т.е. МН  ⊥ ВС
МН по т. Пифагора 
МН=√(АН²+АМ²), где АН - высота из А к стороне ВС. 
S (АВС)=ВС*АН:2
АН=2 S (ABC):BC
По формуле Герона S (ABC)=84 см² ( вычисления не привожу, сделать их несложно, а треугольник со сторонами 13, 14, 15 встречается часто и его площадь поневоле запоминается). 
АН=16*:14=12 см. 
По т. о трех перпендикулярах АН - проекция МН на плоскость Δ АВС. 
МНА -  прямоугольный треугольник из Пифагоровых троек с отношением сторон 5:12:13 ⇒
МН=13 см ( легко проверить по т. Пифагора)
Ответ: Расстояние от М до ВС=13 см.