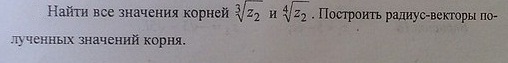Ответы
Ответ дал:
0
|z2|=√(6+6)=√12=2√3
a<0 U b<0⇒φ=-π+arctg1=-π+π/4=-3π/4
![sqrt[3]{z2} = sqrt[6]{12} *(cos1/3*(-3 pi /4+2 pi k)+isin1/3*(-3 pi /4+2 pi k)) sqrt[3]{z2} = sqrt[6]{12} *(cos1/3*(-3 pi /4+2 pi k)+isin1/3*(-3 pi /4+2 pi k))](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7Bz2%7D+%3D+sqrt%5B6%5D%7B12%7D+%2A%28cos1%2F3%2A%28-3+pi+%2F4%2B2+pi+k%29%2Bisin1%2F3%2A%28-3+pi+%2F4%2B2+pi+k%29%29)
k=0
![sqrt[6]{12} *(cos(- pi /4)+isin(- pi /4)) sqrt[6]{12} *(cos(- pi /4)+isin(- pi /4))](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7B12%7D+%2A%28cos%28-+pi+%2F4%29%2Bisin%28-+pi+%2F4%29%29)
k=1![sqrt[]{12}*(cos5 pi /12+isin5 pi /12) sqrt[]{12}*(cos5 pi /12+isin5 pi /12)](https://tex.z-dn.net/?f=+sqrt%5B%5D%7B12%7D%2A%28cos5+pi+%2F12%2Bisin5+pi+%2F12%29+)
k=3![sqrt[6]{12}*cos13 pi /12+isin13 pi /12 sqrt[6]{12}*cos13 pi /12+isin13 pi /12](https://tex.z-dn.net/?f=+sqrt%5B6%5D%7B12%7D%2Acos13+pi+%2F12%2Bisin13+pi+%2F12+)
R≈1.5 рисунок 1
![sqrt[4]{z2} = sqrt[8]{12}*(cos1/4*(-3 pi /4+2 pi n)+isin1/4*(-3 pi /4+2 pi n)) sqrt[4]{z2} = sqrt[8]{12}*(cos1/4*(-3 pi /4+2 pi n)+isin1/4*(-3 pi /4+2 pi n))](https://tex.z-dn.net/?f=+sqrt%5B4%5D%7Bz2%7D+%3D+sqrt%5B8%5D%7B12%7D%2A%28cos1%2F4%2A%28-3+pi+%2F4%2B2+pi+n%29%2Bisin1%2F4%2A%28-3+pi+%2F4%2B2+pi+n%29%29+)
n=0![sqrt[8]{12} (cos(-3 pi /16)+isin(-3 pi /16)) sqrt[8]{12} (cos(-3 pi /16)+isin(-3 pi /16))](https://tex.z-dn.net/?f=+sqrt%5B8%5D%7B12%7D+%28cos%28-3+pi+%2F16%29%2Bisin%28-3+pi+%2F16%29%29)
n=1![sqrt[8]{12} *(cos5 pi /16+isin5 pi /16) sqrt[8]{12} *(cos5 pi /16+isin5 pi /16)](https://tex.z-dn.net/?f=+sqrt%5B8%5D%7B12%7D+%2A%28cos5+pi+%2F16%2Bisin5+pi+%2F16%29)
n=2![sqrt[8]{12} *(cos13 pi /16+isin13 pi /16) sqrt[8]{12} *(cos13 pi /16+isin13 pi /16)](https://tex.z-dn.net/?f=+sqrt%5B8%5D%7B12%7D+%2A%28cos13+pi+%2F16%2Bisin13+pi+%2F16%29)
n=3![sqrt[8]{12}*(cos21 pi /16=isin21 pi /16) sqrt[8]{12}*(cos21 pi /16=isin21 pi /16)](https://tex.z-dn.net/?f=+sqrt%5B8%5D%7B12%7D%2A%28cos21+pi+%2F16%3Disin21+pi+%2F16%29+)
R≈1,4
a<0 U b<0⇒φ=-π+arctg1=-π+π/4=-3π/4
k=0
k=1
k=3
R≈1.5 рисунок 1
n=0
n=1
n=2
n=3
R≈1,4
Приложения:
Ответ дал:
0
z^{1/n} =2√3 (cos(-3π/4+2πk)+isin(-3π/4+2πk), где k=0,1,2,...,n-1
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад