Как построить треугольник за основой, углом при вершине и радиусом вписанной окружности? (Конструктивная геометрия)

Допускаю, что решение не относится к конструктивной геометрии. К простой - относится. Возможно, оно Вам поможет.
Понадобятся :
циркуль, линейка, угольник с прямым углом для построения параллельных прямых, транспортир, карандаш. 
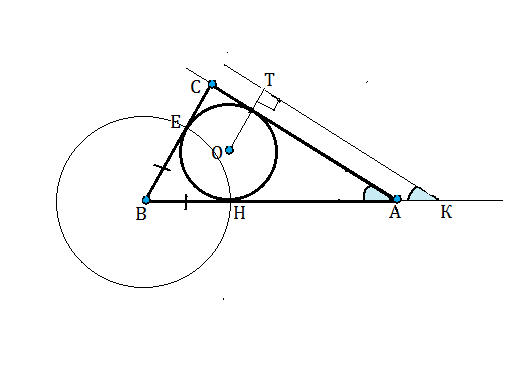
1). Чертим окружность данного радиуса. 
2).Под ней чертим произвольную прямую с точкой касания с окружностью в точке Н. 
3). От Н вправо откладываем НК,  приближенно равную по длине данной стороне.
4). От К как от вершины строим данный угол с помощью транспортира ( или по методике построения угла) 
5). Из центра О проводим к этой стороне угла перпендикуляр ОТ по стандартному методу. 
6). Через точку пересечения ОТ и окружности проводим параллельно КТ касательную к окружности. Точку ее пересечения с прямой НК обозначим А. Это вершина угла заданной величины. 
7). От А откладываем длину данной стороны. Ставим точку В. ВН по свойству касательной из одной точки равен длине отрезка от В до точки касания окружности с третьей стороной.  
8). Раствором циркуля, равным ВН, проводим из В, как из центра, полуокружность до пересечения с окружностью в точке Е. 
9). Из В через т.Е проводим касательную  до пересечения с прямой, проведенной  из вершины А, т.е. со второй стороной угла А. Точка пересечения С будет третьей вершиной треугольника. 
Треугольник  АВС построен.