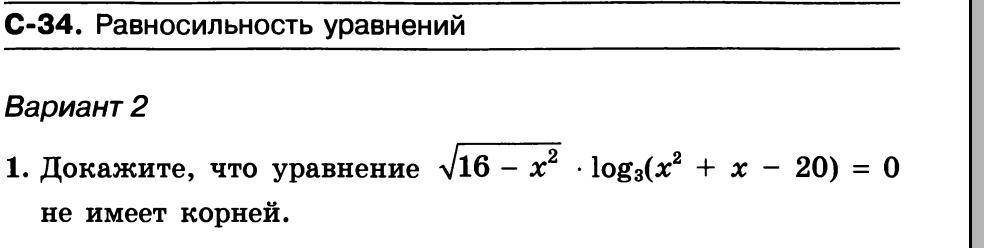Предмет: Алгебра
Автор: Иван7
Вопрос задан 10 лет назад

Докажите, что уравнение не имеет корней

Приложения:

Ответы

Ответ дал: strc

$sqrt{16-x^2}*log_{3}(x^2+x-20)\ 16-x^2 geq 0\ 16-x^2=0\ x^2=16\ x_{1,2}=4;-4\ left [-4;4] right \ x^2+x-20 >0 \ x^2+x - 20 =0\ (x-4)(x+5)=0\ x=4\ x=-5\ left(-infty;-5) cup (4;+infty)right;$

Уравнения не умеют общих решений, что и требовалось доказать.

Следует отметить, что точка 4 не является решением, потому что во втором решении она исключена.

Похожие вопросы

Русский язык

2 года назад

описать картину Ф.П.Толстого "Цветы, фрукты, птица".

Английский язык

2 года назад

Заполни пропуски: To be ..... To do ....... To see

Обществознание

7 лет назад

Сообщение по обществознанию на тему моя внешкольная деятельность. Нужно на завтра.

История

7 лет назад

Перечислите признаки натурально хозяйств

Математика

10 лет назад

Букет роз в 3 раза дороже букета гвоздик. За букет роз заплатили на 50 руб. больше, чем за букет гвоздик. Сколько букетов роз можно купить на 70 рублей?

Алгебра

10 лет назад

При каком значении переменной x верно равенство корень x=11

Алгебра

10 лет назад

для работы в модельном агенстве отбирают кандидаток с ростом не менее 170 см.есть 4 группы кандидаток.В какой из групп заведомо половина кандидаток подходит по росту. Про группы известно

История

10 лет назад

Дайте современые названия следующих географических областей и обьектов. 1) г.Царьград - _______ 2) Варяжское море - _______ 3) Угорская земля - _______ 4) р.Итиль - ________