найдите площадь круга, вписанного в равнобедренную трапецию с большим основание, равным 18 и острым углом 60 градусов.

По условию задачи трапеция равнобедренная.

Следовательно, оба угла при ее основании равны 60°. 
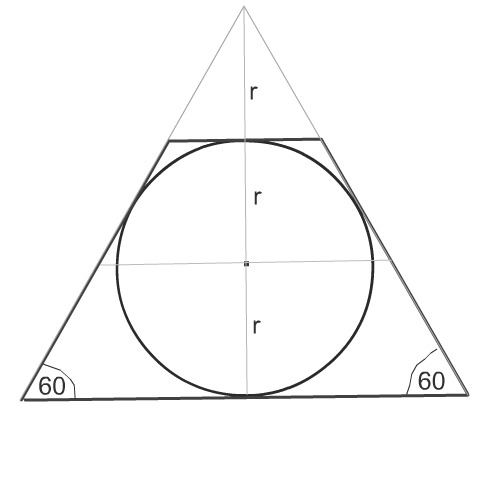
Продолжим боковые стороны трапеции до их пересечения.
Получившийся при этом треугольник - равносторонний.
Радиус окружности, вписанной в равносторонний треугольник, равен одной трети его высоты.
r=h:3
Высоту найдем по формуле высоты правильного треугольника:
h=(а√3):2, где а - сторона этого треугольника.
h=18√3):2=9√3

Радиус вписанной окружности равен:
h:3=3√3
r=3√3
S=πr²=27π