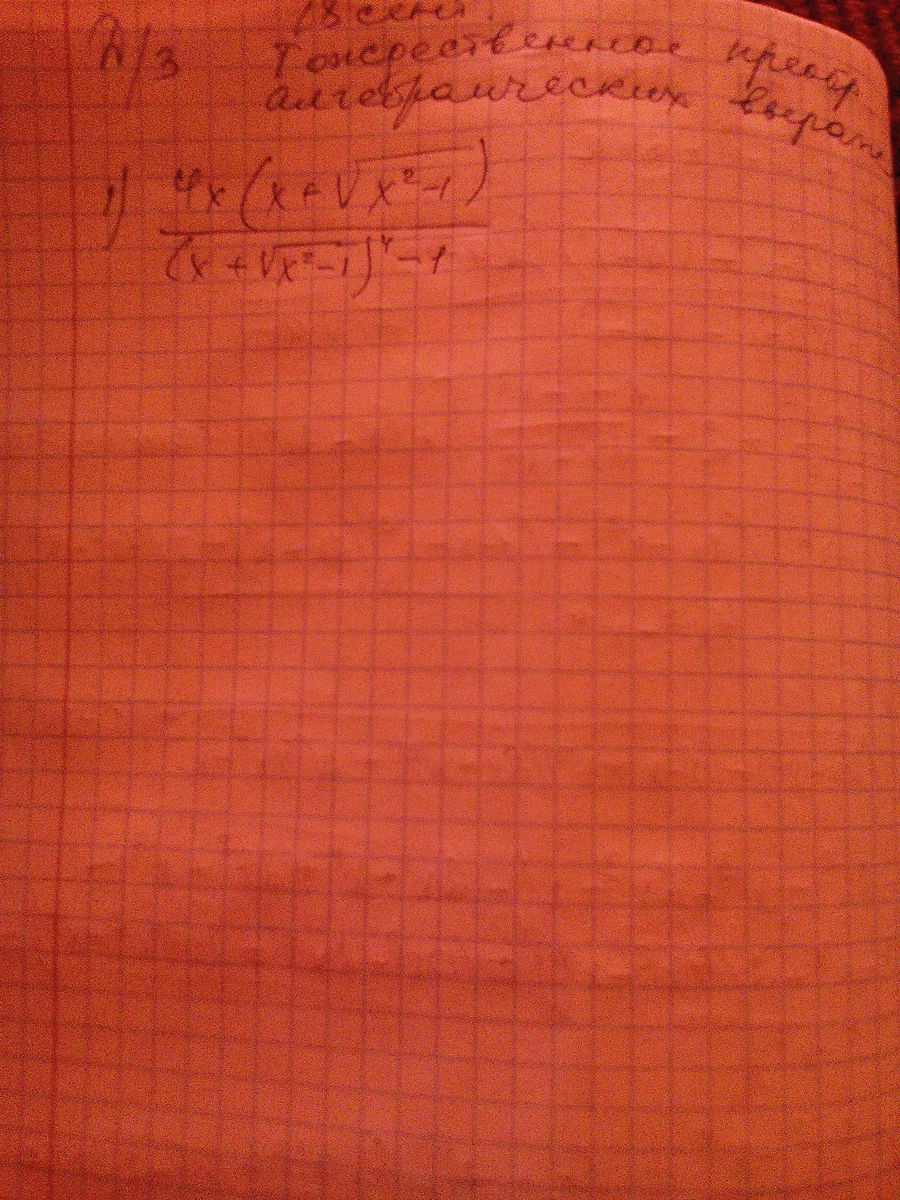• Предмет: Алгебра
  • Автор: ника10678
  • Вопрос задан 9 лет назад
< >

пожалуйста помогите решить тождество

Приложения:

Ответы

Ответ дал: kalbim
0
frac{4x(x+ sqrt{x^{2}-1})}{(x+ sqrt{x^{2}-1})^{4}-1}= frac{4x(x+ sqrt{x^{2}-1})}{((x+ sqrt{x^{2}-1})^{2}-1)((x+ sqrt{x^{2}-1})^{2}+1)}=frac{4x(x+ sqrt{x^{2}-1})}{(x+ sqrt{x^{2}-1}-1)(x+ sqrt{x^{2}-1}+1)((x+ sqrt{x^{2}-1})^{2}+1)}=frac{4x(x+ sqrt{x^{2}-1})}{(x+ sqrt{x^{2}-1}-1)(x+ sqrt{x^{2}-1}+1)(x^{2}+ 2x*sqrt{x^{2}-1}+x^{2}-1+1)}=frac{4x(x+ sqrt{x^{2}-1})}{(x+ sqrt{x^{2}-1}-1)(x+ sqrt{x^{2}-1}+1)(2x^{2}+ 2x*sqrt{x^{2}-1})}=frac{4x(x+ sqrt{x^{2}-1})}{2x(x+ sqrt{x^{2}-1}-1)(x+ sqrt{x^{2}-1}+1)(x+sqrt{x^{2}-1})}=frac{2}{(x+ sqrt{x^{2}-1}-1)(x+ sqrt{x^{2}-1}+1)}=frac{2}{((x+ sqrt{x^{2}-1})^{2}-1)}
Ответ дал: ника10678
0
спасибо большое ,но очень сложно .Я ничего не поняла
Ответ дал: kalbim
0
по-другому, в принципе, никак. Используются формулы сокращенного умножения, а именно: разность квадратов и квадрат суммы
Похожие вопросы
Математика
2 года назад
Как решить уравнение 36×(x-3)=10-2×(x+2)
Математика
2 года назад
найдите значение выражения.61,3х если х=8,х=42,х=100. 5класс
Математика
7 лет назад
Знайдіть радіус кола, описаного навколо правильного шестикутника із стороною 2,5см. Обчисліть довжину кола і площу круга.
Химия
7 лет назад
Отметьте, при взаимодействии каких веществ происходит реакция ионного обмена с выделением углекислого газа: гидрокарбонат бария и серная кислота карбонат натрия и азотная кислота карбонат бария
Химия
9 лет назад
запишите уравнения реакций магния с: Кислородом,хлором Cl2, серой, азотом N2,соляной кислотой...
Алгебра
9 лет назад
Упростите выражение: 3(2а-5)-4(1-3а)+5а
Химия
10 лет назад
При сжигании газообразного углеводорода с плотностью по водороду 21 получено 8,4 л оксида углерода (IV) (н.у.) и 6,75 г воды. Определите формулу углеводорода
Биология
10 лет назад
Остров Врангеля 1)Растительный мир