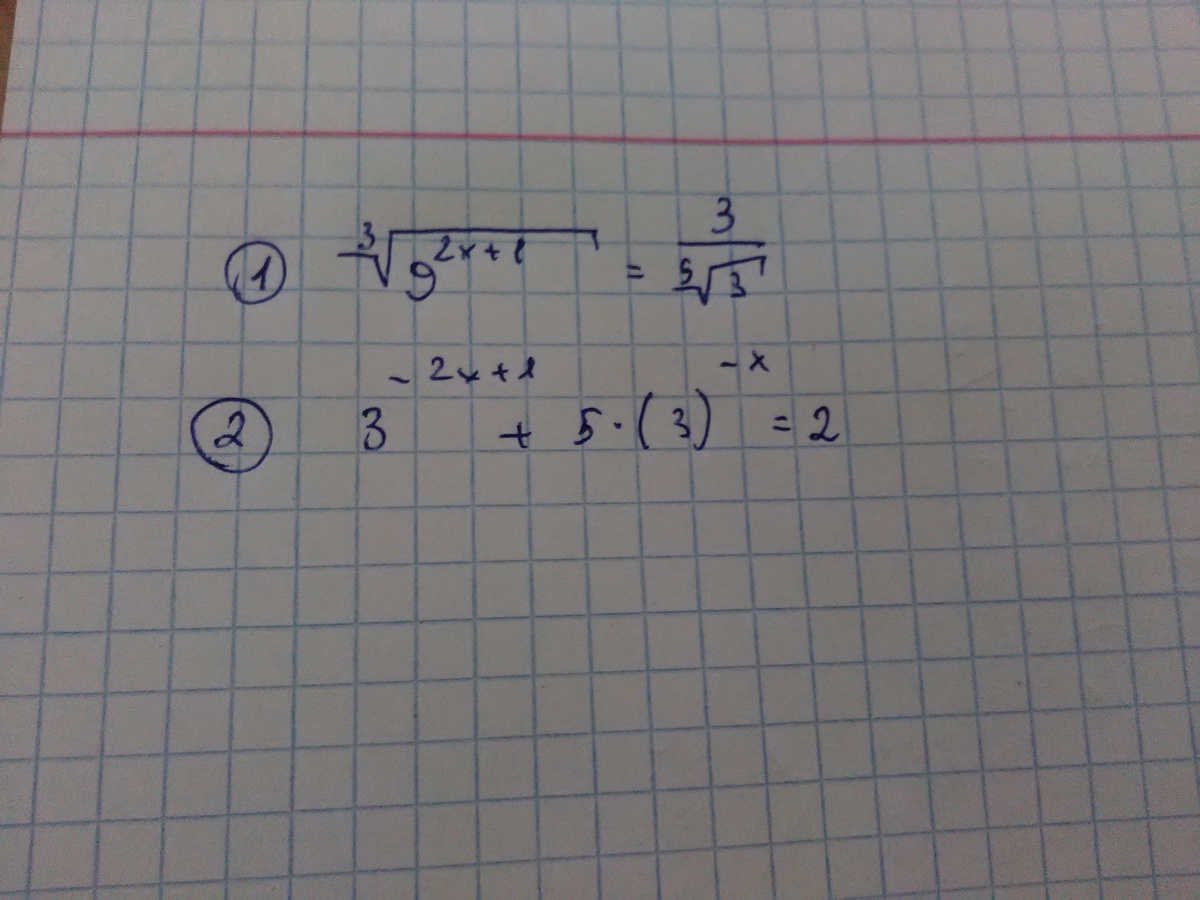Ответы
Ответ дал:
0
1) ![sqrt[3]{9 ^{2x+1} } = frac{3}{ sqrt[5]{3} } sqrt[3]{9 ^{2x+1} } = frac{3}{ sqrt[5]{3} }](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B9+%5E%7B2x%2B1%7D+%7D+%3D+frac%7B3%7D%7B+sqrt%5B5%5D%7B3%7D+%7D+)
Преобразуем степени:

В равенстве при равных основаниях показатели степени равны:

10х + 10 = 12
10х = 12 - 10 = 2
х = 2/10 = 1/5.
2)

Произведём замену:
 .
.
Тогда получаем квадратное уравнение:
3у² + 5у - 2 = 0.
Квадратное уравнение, решаем относительно y:
Ищем дискриминант:D=5^2-4*3*(-2)=25-4*3*(-2)=25-12*(-2)=25-(-12*2)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:
y₁=(√49-5)/(2*3)=(7-5)/(2*3)=2/(2*3)=2/6=1/3;
y₂=(-√49-5)/(2*3)=(-7-5)/(2*3)=-12/(2*3)=-12/6=-2.
Второй отрицательный корень отбрасываем по ОДЗ.
Производим обратную замену:
 .
.
Отсюда ответ: х = 1.
Преобразуем степени:
В равенстве при равных основаниях показатели степени равны:
10х + 10 = 12
10х = 12 - 10 = 2
х = 2/10 = 1/5.
2)
Произведём замену:
Тогда получаем квадратное уравнение:
3у² + 5у - 2 = 0.
Квадратное уравнение, решаем относительно y:
Ищем дискриминант:D=5^2-4*3*(-2)=25-4*3*(-2)=25-12*(-2)=25-(-12*2)=25-(-24)=25+24=49;
Дискриминант больше 0, уравнение имеет 2 корня:
y₁=(√49-5)/(2*3)=(7-5)/(2*3)=2/(2*3)=2/6=1/3;
y₂=(-√49-5)/(2*3)=(-7-5)/(2*3)=-12/(2*3)=-12/6=-2.
Второй отрицательный корень отбрасываем по ОДЗ.
Производим обратную замену:
Отсюда ответ: х = 1.
Ответ дал:
0
Я даже боюсь спросить, а это точно правильно?)
Ответ дал:
0
Так по готовому уже можно и самому проверить - правильно или нет!!!
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад