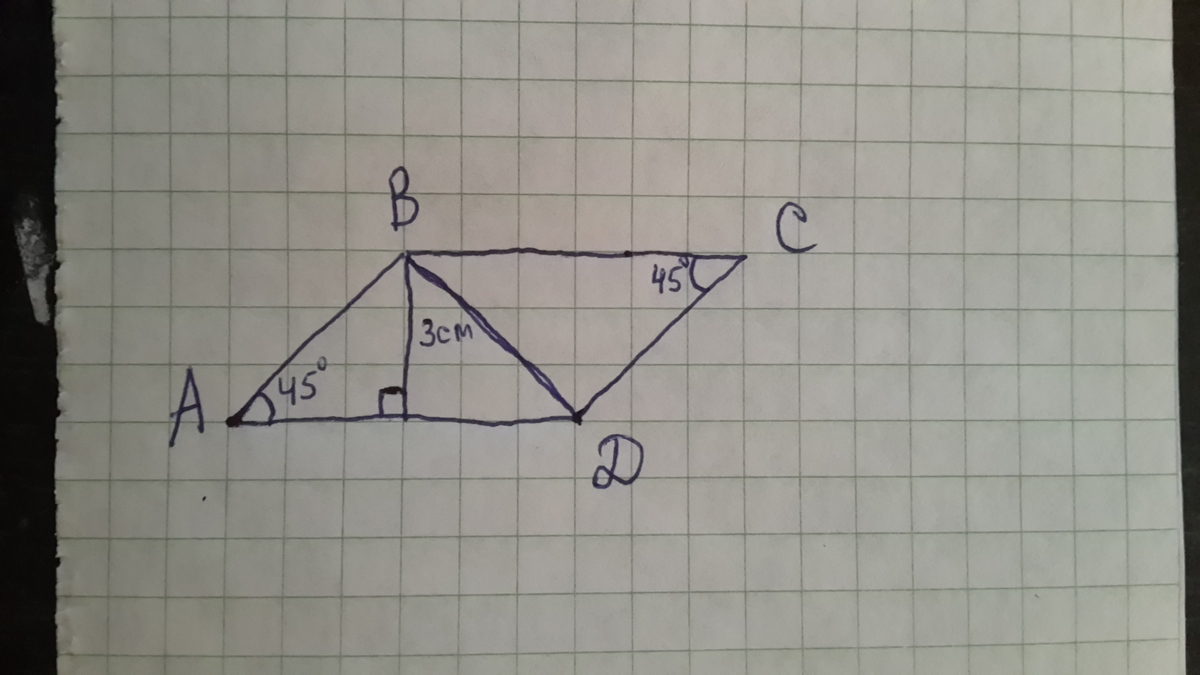
Один из углов параллелограмма равен 45 градусов. Высота параллелограмма, проведённая из вершины его тупого угла, равна 3 см, делит сторону параллелограмма пополам. Найдите эту сторону параллелограмма и углы, которые образует диагональ, соединяющая вершины тупых углов со сторонами параллелограмма.
Ответы
Ответ дал:
0
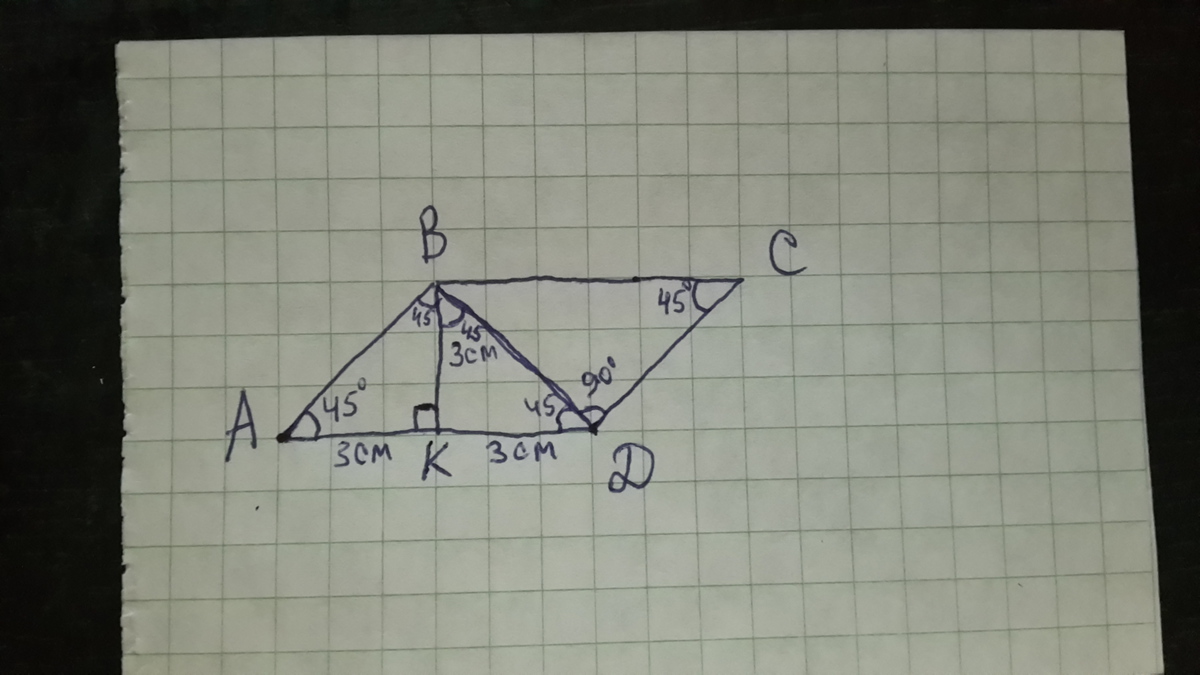
Найдём ∠ABK 90-45=45° отсюда следует ABK равнобедренный треугольник BK=AK, а зная что BK делит сторону пополам мы находим эту сторону
3*2=6см это AD
И теперь углы: ΔABK=ΔKBD отсюда∠ABD=45+45=90° из свойств параллелограмма ∠ABD=∠BDC=90
∠DBC=∠ADB По свойствам параллелограмма
3*2=6см это AD
И теперь углы: ΔABK=ΔKBD отсюда∠ABD=45+45=90° из свойств параллелограмма ∠ABD=∠BDC=90
∠DBC=∠ADB По свойствам параллелограмма
Приложения:
Похожие вопросы
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад