ПОМОГИТЕ С ГЕОМЕТРИЕЙ,ПОЖАЛУЙСТА!
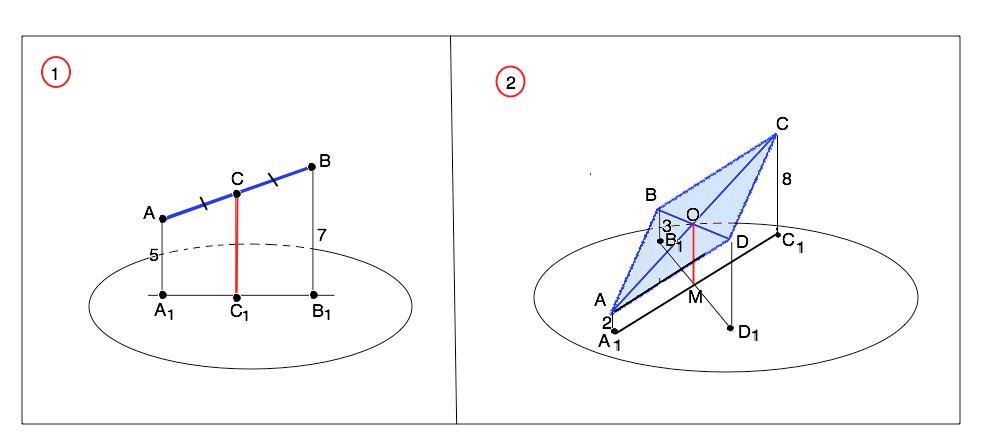
1.AB не пересекает α;AC=CB;AA1∥СС1∥BB1; AA1=5; BB1=7. Найти:CC1
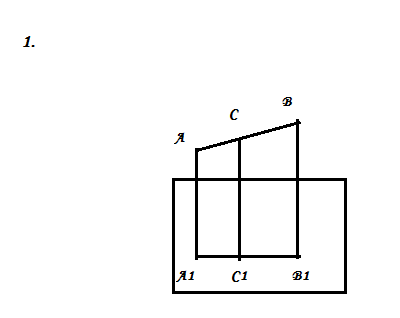
2.ABCD-параллеограмм,AA1∥BB1∥CC1∥DD1
AA1=2, BB1=3, CC1=8. Найти:DD1.
Ответы
1) Боковые стороны четырехугольника АА1В1В параллельны по условию, ⇒ АА1В1В - трапеция. Т.к. АС=СВ и СС1║АА1║ВВ1, СС1 - средняя линия трапеции и равна полусумме её оснований.
СС1=(АА1+ВВ1):2=(5+7):2=6
2) ABCD – параллелограмм. Через вершины параллелограмма проведены параллельные прямые, пересекающие некую плоскость в точках А1, В1, С1 и D1. Длина АА1 = 2, ВВ1 = 3, СС1 = 8
Найти длину отрезка DD1.
Решение:
Проведем диагонали АС и ВD параллелограмма и их проекции А1С1 и В1D1 на плоскости . Диагонали параллелограмма пересекаются в их середине. АО=ОВ, ВО=ОD, следовательно, и в их проекциях А1М=МС1 и В1М=МD1. Т.к. АА1║СС1, четырехугольник АА1С1С - трапеция. ОМ=(АА1+СС1):2=(2+8):2=5. Аналогично ВВ1D1D - трапеция и ОМ - её средняя линия. Поэтому ВВ1+DD1=2ОМ=10. Тогда DD1=2ОМ-ВВ1=10-3=7 (ед. длины).