Дано выражение y=f(x), где f(x) =
Найдите значения переменной, при которых
f(x) < 0

Решается методом интервалов. Для начала находим D(f) и нули функции:

D(f): x(2x+1)≠0
x≠0 и 2x+1≠0
x≠0 и x≠-1/2

f(x)=0 
Умножаем все выражение на x(2x+1), для x≠0 и x≠-1/2, получаем:
(x+2)²(x-1)(2x+3)=0
(x+2)²=0 или x-1=0 или 2x+3=0
x=-2 или x=1 или x=-3/2
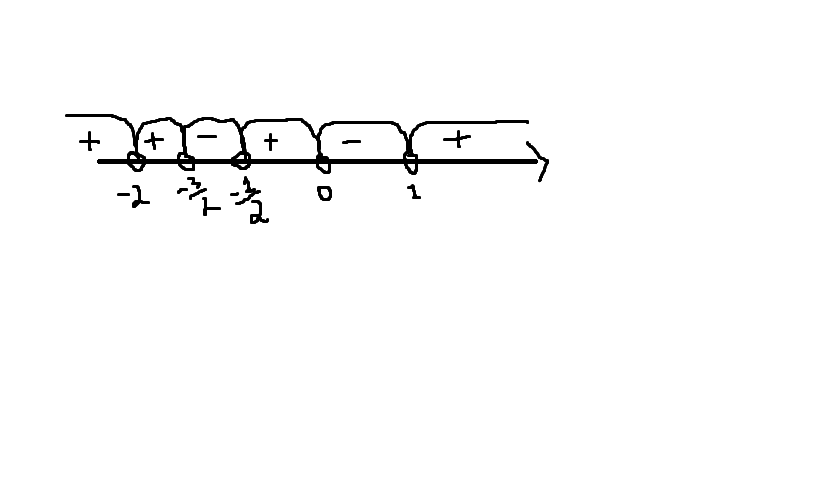
Наносим все полученный точки на прямую и вычисляем знаки на интервалах.
Вложение.
Рассмотрим при x>1. Берём 100 и получаем + на интервале. Дальше знаки чередуются вплоть до -2, т.к. -2 это корень выражения (x+2)². При возведении числа в чётную степень знак числа не меняется, значит и у нас знак интервала не поменяется.
Там где минус f(x)<0. Итого получаем отрезок
x∈(-3/2;-1/2)U(0;1)

спасибо огромное!)