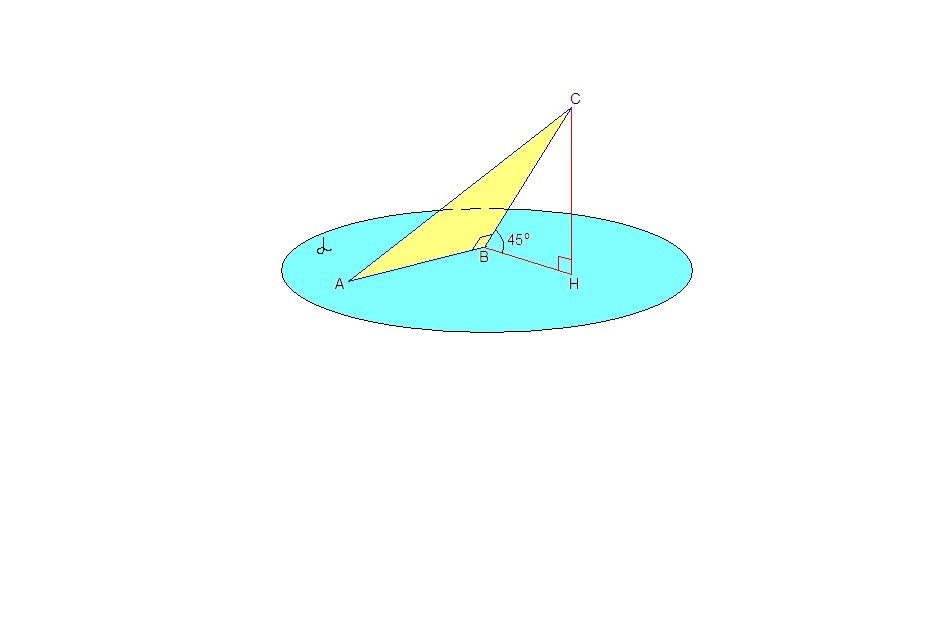
Катет AB прямоугольного треугольника ABC (угол B=90°) лежит в плоскости α. Найдите расстояние от точки С до плоскости α, если AC = 17 см, AB = 15 см, а двугранный угол между плоскостями ABC и α равен 45°.

Расстояние от точки С до плоскости α - перпендикуляр к плоскости - отрезок СН.

СВ⊥АВ так как ΔАВС прямоугольный,
НВ - проекция СВ на плоскость α, ⇒
НВ⊥АВ по теореме, обратной теореме о трех перпендикулярах.
Значит, ∠СВН = 45° - линейный угол двугранного угла между плоскостью треугольника и плоскостью α.

Из ΔАВС по теореме Пифагора:
СВ = √(АС² - АВ²) = √(289 - 225) = √64 = 8 см

ΔСНВ прямоугольный равнобедренный, по теореме Пифагора
СВ² = СН² + НВ² = 2СН²
64 = 2СН²
СН = √32 = 4√2 см