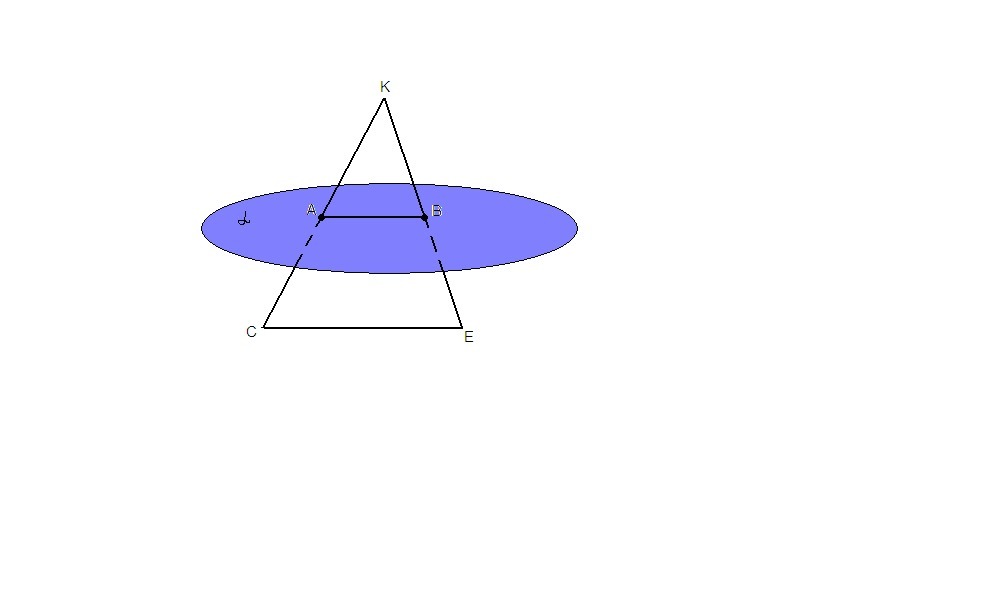
Середины сторон СК и ЕК треугольника СЕК лежат в плоскости a , а сторона СЕ не лежит в этой
плоскости. Докажите, что прямая СЕ ||a .

Пусть А - середина КС, В - середина КЕ. Тогда АВ - средняя линия треугольника СКЕ. ⇒ АВ║СЕ.
Если две точки прямой лежат в плоскости, то и прямая лежит в плоскости.
Прямая АВ - линия пересечения плоскости треугольника СКЕ и плоскости α.
СЕ║АВ, АВ ⊂ α,    ⇒ СЕ║α.