Здравствуйте. Помогите с доказательством тригонометрического выражения!
У меня при решении получается -cos^2t.
cos^2(pi-t)=-cos^2t;
sin^2(pi/2-t)=cos^2t;
cos(pi+t)=-cost;
cos(2pi-t)=cost;
tg^2(t-pi/2)=-ctg^2t;
ctg^2(3pi/2+t)=-tg^2t;
В конечном итоге имею в знаменателе 1, а в числителе -cos^2t.
В чём моя ошибка?
Прошу прощения что не использую редактор кодов, но он при выборе элементов перезагружает страницу!
Приложения:
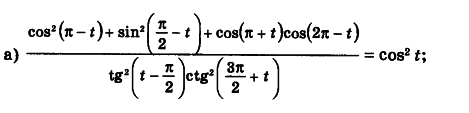
Ответы
Ответ дал:
0
cos^2(pi-t)=-cos^2t;
sin^2(pi/2-t)=cos^2t;
cos(pi+t)=-cost;
cos(2pi-t)=cost;
tg^2(t-pi/2)=ctg^2t;
ctg^2(3pi/2+t)=tg^2t;
(cos²t+cos²t+(-cost)*cost)/ctg²t*tg²t=(2cos²t-cos²t)/1=cos²t
sin^2(pi/2-t)=cos^2t;
cos(pi+t)=-cost;
cos(2pi-t)=cost;
tg^2(t-pi/2)=ctg^2t;
ctg^2(3pi/2+t)=tg^2t;
(cos²t+cos²t+(-cost)*cost)/ctg²t*tg²t=(2cos²t-cos²t)/1=cos²t
Ответ дал:
0
Почему ctg^2(3pi/2+t)=tg^2t;? Ведь при наличии выражения в виде 3pi/2 в частности происходит изменение наименования тригонометрической функции, а знак ставится такой, если бы в преобразуемой функции 0<t<pi/2. Ctg^2 в таком случае будет находится в третьей четверти, где знак ctg отрицателен!
Ответ дал:
0
*в четвёртой четверти.
Ответ дал:
0
Ошибку понял. Я не обратил внимание на то, что ф-ция записана в квадрате...
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад