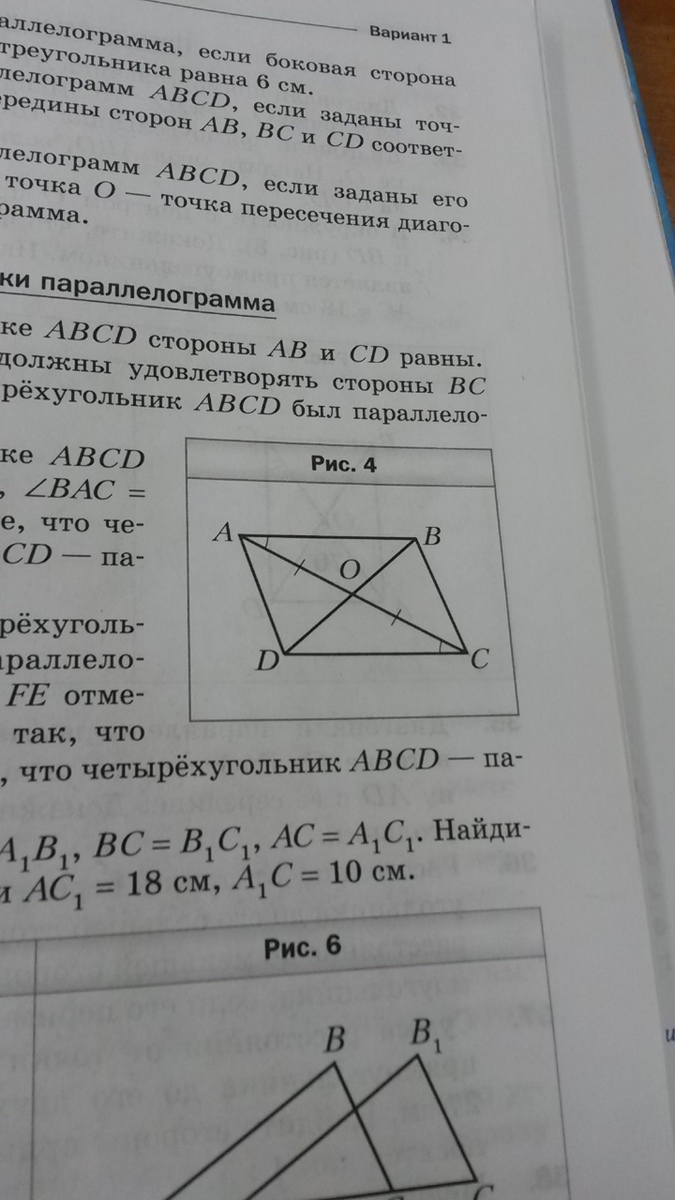
В четырехугольнике ABCD AO=OC, угол BAC = углу ACD. Докажите, что четырехугольник ABCD - параллелограмм.
Приложения:
Ответы
Ответ дал:
0
ΔAOB = ΔCOD по стороне и двум углам прилежащим к ней (∠AOB=∠COD как вертикальные; AO=CO и ∠BAO=∠DCO по условию). Поэтому, AB = CD.
∠BAC и ∠ACD накрестлежащие углы при прямых AB, CD и секущей AC. ∠BAC = ∠ACD ⇒ AB║CD.
В четырёхугольнике ABCD: AB=CD и AB║CD. Значит, ABCD - параллелограмм, что и требовалось доказать.
Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад