На боковых сторонам равнобедренного треугольника АВС с основанием АС отложены равные отрезки АМ и СN. ВD медиана треугольника АВС-пересекает отрезок МN в точке О. Докажите что ВО- медиана треугольника МВN.
Приложения:
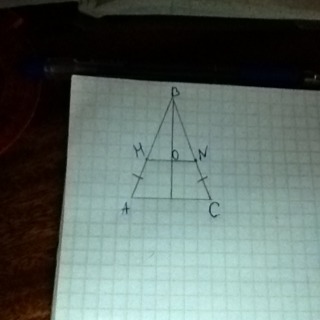
Ответы
Ответ дал:
0
В треугольнике АВС МВ=ВN т.к. треугоник равнобедренный, а если АМ=СN, то и другие части тоже равны. Медиана в равнобедренном треугонике является еще и биссектрисой,значит угол МВО равен углу ОВN. Докажем что треугольники МВО и ОВN равны по двум сторонам и углу между ними: ВО- общая сторона, угол МВО равен углу ОВN, сторона МВ равна ВN. Так как треугольники равны то сторона МО равна ВN, следовательно ВО будет медианой.
Похожие вопросы
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад