Острые углы прямоугольного треугольника равны 85 и 5.Найдите угол между высотой и биссектрисой,проведенными из вершины прямого угла.Ответ дайте в градусах
Картинка внутри!
Приложения:
Ответы
Ответ дал:
0
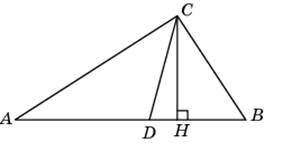
Предположим,что угол B=85 градусов. Треугольник CHB - прямоугольный.=> угол HCB=180-(90+85)=5 градусам. CD - биссектриса => угол ACD = углу DCB = 45 градусов (90/2=45). Рассмотрим полученые данные: угол DCB=45 градусов,угол HCB=5 градусов => угол DCH = угол DCB-уголHCB.
DCH=45-5=40.
Если предположить,что угол B равен 5 градусам,решать идентично,получится лишь другое число.
Ответ дал:
0
уголВ=85, угол А=5
Рассмотрим трАСН, уголСНА=90, уголСАН=5, уголНСА=85
уголDCA=45, т.к.СD биссектриса прямого угла
угол НСD=уголНСА-уголDСА=85-45=40
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад