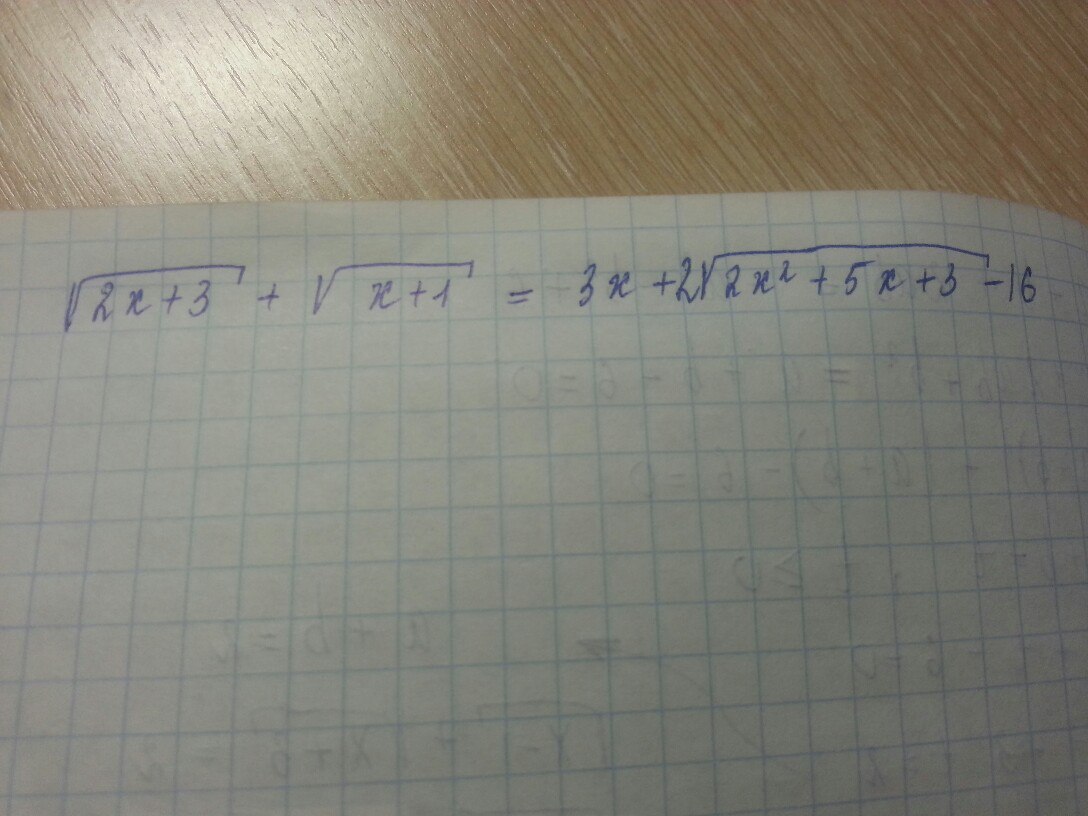Помогите решить , срочно! методом замены

Уравнение примет вид:

u+v=u²+v²-4+2uv-16
u+v=(u+v)²-20
(u+v)²-(u+v)-20=0
это квадратное уравнение относительно (u+v).
D=1+80=81
u+v=5          или    u+v=-4 не удовлетворяет условию   u≥0    v≥0
Решаем уравнение:



ОДЗ: х≥-1
Возводим в квадрат
2х+3+2√(2х²+5х+3)+х+1=25
2√(2х²+5х+3)=21-3х
Возводим в квадрат при условии, что 21-3х≥0      или    х≤7
4(2х²+5х+3)=441-126х+9х²
х²-146х+429=0
D=146²-4·429=21316-1716=19600=140²
x=(146-140)/2=3      или     х=(146+140)/2=143 - не удовлетворяет условию
                                         х≤7   

Ответ. х=3

после слов: уравнение примет вид, там разве не +2uv?

да +, далее все верно