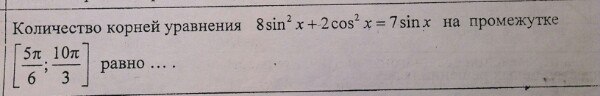Предмет: Алгебра
Автор: kryapta
Вопрос задан 9 лет назад

< >

Помогите решить пример

Приложения:

Ответы

Ответ дал: kalbim

0

$8sin^{2}x+2*(1-sin^{2}x)-7sinx=0$
$8sin^{2}x+2-2sin^{2}x-7sinx=0$
$6sin^{2}x-7sinx+2=0$

Замена: sinx=t∈[-1;1]

$6t^{2}-7t+2=0, D=49-4*2*6=1$
$t_{1}= frac{7-1}{12}=frac{1}{2}$
$t_{2}= frac{7+1}{12}=frac{2}{3}$

Вернемся к замене:
1) $sinx=frac{1}{2}$
$x=frac{ pi }{6}+2 pi k$ , k∈Z
$x=frac{5 pi }{6}+2 pi k$ , k∈Z
2) $sinx=frac{2}{3}$
$x=arcsin(frac{2}{3})+2 pi k$ , k∈Z
$x= pi -arcsin(frac{2}{3})+2 pi k$ , k∈Z

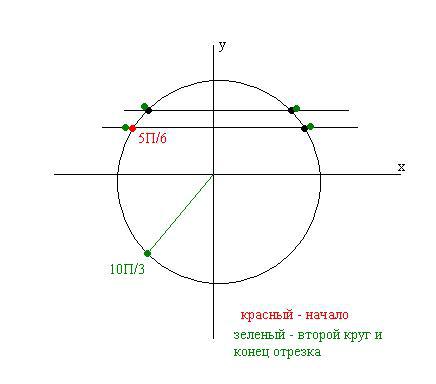
Отметим решения на единичной окружности и найдем их количество на заданном отрезке (см. рисунок).

Ответ: 5 корней

Приложения:

Похожие вопросы

Обществознание

2 года назад

он может быть морским, серым,злым,а может быть в овечьей шкуре им можно смотреть или выть но работать им ни когда не станет кто же он?

Физика

2 года назад

. Электрический пробой в воздухе происходит, если модуль напряженности поля достигает 3 МВ/м. Какое максимальное напряжение (кВ) можно подать на пластины конденсатора в воздухе, если расстояние между

Алгебра

7 лет назад

Точка H является основанием высоты,проведенной из вершины прямого угла C треугольника ABC к гипотенузе AB.Найдите BC,если BH=4.8 и AB=13 1/3(тринадцать целых одна третья)

География

7 лет назад

Помогите пожалуйста ответьте на вопрос. Подберите, с помощью разных источников, изображения миража, гало, полярного сияния, огней святого Эльма

Литература

9 лет назад

какого цвета колобок

Математика

9 лет назад

В шахматном турнире участвовало 7 человек. Каждый участник сыграл с каждым по одной партии. Сколько всего партий было сыграно в шахматном турнире?

Биология

10 лет назад

что такое промежуточный хозяин

Математика

10 лет назад

найдите значение выражения , применив распределительное свойство умножения : а) (250+25)*4 б) 6*(150+16) в) 8*11+8*29 г) 36*184+36*816