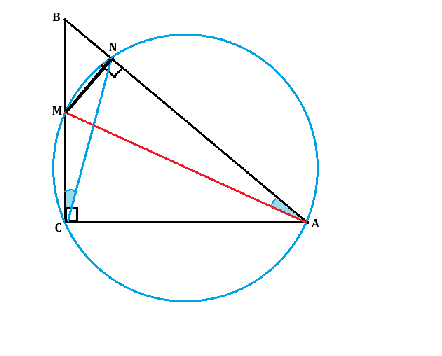
С точки М катета ВС прямоугольного треугольника АВС на гипотенузу АВ опущен перпендикуляр MN. Доказать, что углы MAN и MCN равны

У прямоугольных треугольников МСА и МNА общая гипотенуза АМ. Следовательно, эта гипотенуза будет диаметром описанной вокруг них окружности. Тогда углы МСN и МАN  вписанные и опираются на одну и ту же дугу, стягиваемую хордой МN. 
Если вписанные в окружность углы опираются на одну и ту же дугу  ( или на равные дуги) - эти углы равны, что и требовалось доказать.