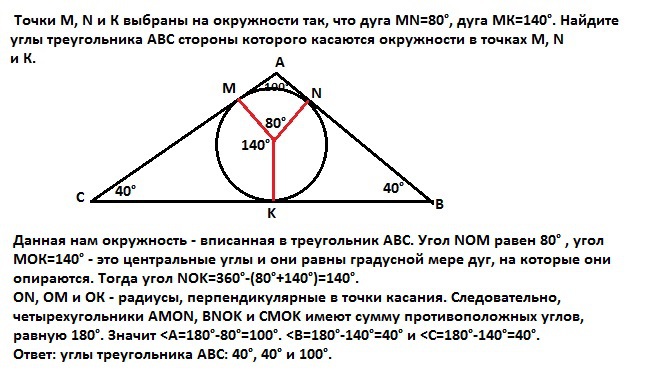
Точки М, N и К выбраны на окружности так, что дуга МN=80°, дуга МК=140°. Найдите углы треугольника АВС стороны которого касаются окружности в точках М, N и К.

Данная нам окружность - вписанная в треугольник АВС. Угол NOM равен 80° , угол МОК=140° - это центральные углы и они равны градусной мере дуг, на которые они опираются. Тогда угол NOK=360°-(80°+140°)=140°.
ОN, OM и ОК - радиусы, перпендикулярные в точки касания. Следовательно, четырехугольники АMON, BNOK и CMOK имеют сумму противоположных углов, равную 180°. Значит <A=180°-80°=100°. <B=180°-140°=40° и <C=180°-140°=40°.
Ответ: углы треугольника АВС: 40°, 40° и 100°.