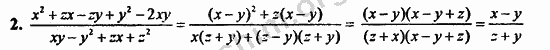Ответы
Ответ дал:
0
В знаменателе дано выражение :
x^2 + zx - zy + y^2 - 2zy =x^2-2zy+y^2+zx-zy отчётливо просматривается квадрат разности и то, что можно вынести z за скобку.
= (x-y)^2 +z(x-y). Далее мы можем вынести х - у за скобку ...
=(x-y)(x-y+z)
Далее перейдём к числителю :
xy-y^2+zx+z^2=xy+zx+z^2-y^2 = сразу видно то, что можно вынести х за скобку и разность квадратов = x(z+y)+(z+y)(z-y) = далее можем вынести за скобки z+y =(z+y)(x-y+z)
теперь получается преобразованная дробь.
(x-y)(x-y+z)/(z+y)(z-y+z)=сокращаем = (x-y)/(z+y)
x^2 + zx - zy + y^2 - 2zy =x^2-2zy+y^2+zx-zy отчётливо просматривается квадрат разности и то, что можно вынести z за скобку.
= (x-y)^2 +z(x-y). Далее мы можем вынести х - у за скобку ...
=(x-y)(x-y+z)
Далее перейдём к числителю :
xy-y^2+zx+z^2=xy+zx+z^2-y^2 = сразу видно то, что можно вынести х за скобку и разность квадратов = x(z+y)+(z+y)(z-y) = далее можем вынести за скобки z+y =(z+y)(x-y+z)
теперь получается преобразованная дробь.
(x-y)(x-y+z)/(z+y)(z-y+z)=сокращаем = (x-y)/(z+y)
Ответ дал:
0
решение смотри в приложении
Приложения:

Похожие вопросы
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад