Предмет: Алгебра
Автор: mariana23
Вопрос задан 9 лет назад

Номер 2. Найти f'(x) и f'(x0), если:
а) f(x)=2x+1/x-3
б) f(x)=5(затем цифра 5 над корнем)и в корне x^3
в) f(x)=5^х
г) f(x)=корень2х-1

Приложения:

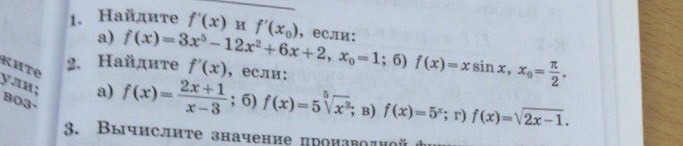
Ответы

Ответ дал: NNNLLL54

$f(x)=frac{2x+1}{x-3}; ,f'(x)=frac{2(x-3)-(2x+1)}{(x-3)^2}=frac{-7}{(x-3)^2}\\f(x)=5sqrt[5]{x^3}; ,; f'(x)=5cdot frac{3}{5}x^{-frac{2}{5}}=frac{3}{sqrt[5]{x^2}}\\f(x)=5^{x}; ,; f'(x)=5^{x}cdot ln5\\f(x)=sqrt{2x-1}; ,; f'(x)=frac{2}{2sqrt{2x-1}}$

$2); f(x)=3x^5-12x^2+6x+2; ,; f'(x)=15x^4-24x+6\\f'(1)=15-24+6=-3\\\f(x)=xcdot sinx; ,; f'(x)=sinx+xcdot cosx\\f'(frac{pi}{2})=sinfrac{pi}{2}+frac{pi}{2}cdot cosfrac{pi}{2}=1+0=1\$

Похожие вопросы

Химия

2 года назад

Какой объем углекислого газа выделится при взаимодействии 15 г карбоната натрия, содержащего 10% примесей, с соляной кислотой? даю 30 баллов!!!

Литература

2 года назад

Какой общий заголовок вы бы дали к этим стихотворениям агнии барто

Химия

7 лет назад

СРОЧНО!!!!! 1)В предложенном перечне отыщите название электролита, при диссоциации которого в качестве анионов образуются только гидроксид-ионы: гидроксид натрия нитрат натрия сероводородная

Геометрия

7 лет назад