• Предмет: Геометрия
  • Автор: hazzahazza
  • Вопрос задан 10 лет назад
< >

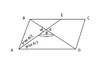
В параллелограмме ABCD, AE-биссектриса <A. AB относится к BC, как 4 к 9.AE-пересекает  диагональ BD в точке К. Найти отношение ВК : КD

Ответы

Ответ дал: lizaliza453
0

АВ/ВС=4/9, притом AB=CD, BC=AD

Используя теорему синусов, составим следующие соотношения:

BK/sin(∠A/2)=AB/sinα

KD/sin(∠A/2)=AD/sinβ=AD/sin(180°-α)=AD/sinα

 

BK=(AB*sin(∠A/2))/sinα

KD=(AD*sin(∠A/2))/sinα

 

делим:

BK/KD=AB/AD=AB/BC=4/9

Приложения:
Похожие вопросы
Английский язык
2 года назад
Correct (+) or not (-) Нужно не правильные в правильные сделать Вот не правельные, помогите сделать в правильные! 1) Are you smoking? No, never.  2) John cooks dinner just now. 3) I'm going skiing
Русский язык
2 года назад
Подберите антонимы к разным значениям следующих многозначных слов; укажите, к каким частям речи относятся антонимы: Великий, глубокий, добро. Брать, выйти, ловко, нежно.
Физика
7 лет назад
Выберите формулу для расчета скорости тела при прямолинейном неравномерном движении
Алгебра
7 лет назад
даю 16 баллов!!Быстрей пж
Химия
10 лет назад
Составить формулы веществ, получающихся в результате реакции (валентности элементов указаны), и поставьте коэффициенты в уравнения:              3 2                 2               52 a)Al+S--AlS
Обществознание
10 лет назад
Помогите пожалуйста, я ва очень сильно прошу, очень срочно нужно!! пожалуйста! Небольшое сочинение! Создать свою фирму. представить себя предпринемателем.
Алгебра
10 лет назад
Из города А в город В выехал автобус. Спустя 0,5 ч вслед за ним из пункта А выехал автомобоиль. через 1.1 ч после своего выхода он, обогнав автобус, находился на расстоянии 2 км от него. Найдите
Математика
10 лет назад
2:вычслите 1)(3,65-2 3/4):3+17/40*12= 2)(9/4+1 17/20):1 7/8+24*3/8=   помогите!!!!!!!!!!!!!!!!!