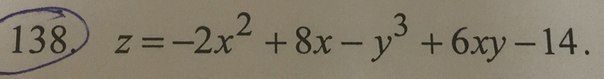Ответы
Ответ дал:
0
Определяю функцию двух переменных:

Нахожу стационарные точки (необходимое условие наличия экстремума):

Необходимое условие: - стационарная точка
- стационарная точка 
Другими словами: обе частных производных должны равнятся нулю. Получили систему уравнений с двумя неизвестными:

Решаю систему:


Стационарные точки:
Определяю Гессиан:

Условие экстремума: если - есть экстремум.
- есть экстремум.
Более того, если - получен минимум
- получен минимум
 - получен максимум.
- получен максимум.
Вариант - ответа не даёт, нужно искать другой способ проверки для данной точки
- ответа не даёт, нужно искать другой способ проверки для данной точки
Если - экстремума нет.
- экстремума нет.
В ншем случае, детерминант гессиана:


Ответ: одна точка экстремума - локальный максимум.
- локальный максимум.
Нахожу стационарные точки (необходимое условие наличия экстремума):
Необходимое условие:
Другими словами: обе частных производных должны равнятся нулю. Получили систему уравнений с двумя неизвестными:
Решаю систему:
Стационарные точки:
Определяю Гессиан:
Условие экстремума: если
Более того, если
Вариант
Если
В ншем случае, детерминант гессиана:
Ответ: одна точка экстремума
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад