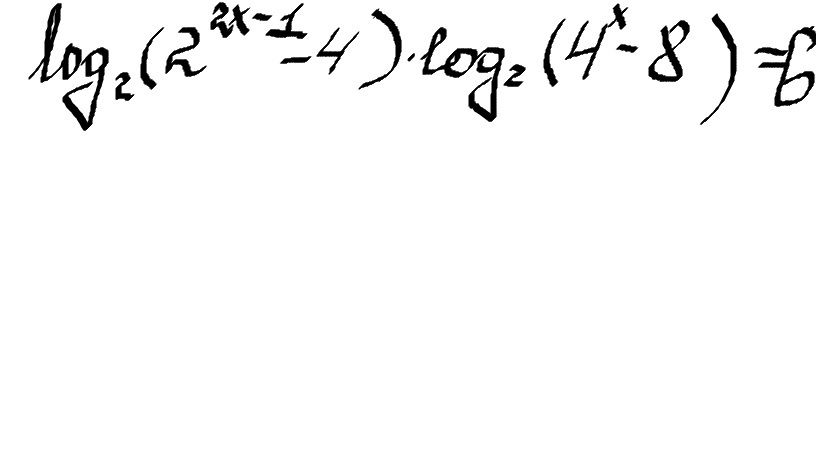Ответы
Ответ дал:
0
ОДЗ 2^(2x-1)>4⇒2x-1>2⇒2x>3⇒x>1,5
4^x>8⇒2^2x>8⇒2x>3⇒x>1,5
x∈(1,5;∞)
![log(2)[(4^x-8)/2]*log(2)(4^x-8)=6](https://tex.z-dn.net/?f=log%282%29%5B%284%5Ex-8%29%2F2%5D%2Alog%282%29%284%5Ex-8%29%3D6 "log(2)[(4^x-8)/2]*log(2)(4^x-8)=6")
(a-1)*a-6=0
a²-a-6=0
a1+a2=1 U a1*a2=-6
a1=-2⇒log(2)(4^x-8)=-2⇒4^x-8=1/4⇒4^x=8 1/4⇒x=log(4)33-1
a2=3⇒log(2)(4^x-8)=3⇒4^x-8=8⇒4^x=16⇒x=2
4^x>8⇒2^2x>8⇒2x>3⇒x>1,5
x∈(1,5;∞)
(a-1)*a-6=0
a²-a-6=0
a1+a2=1 U a1*a2=-6
a1=-2⇒log(2)(4^x-8)=-2⇒4^x-8=1/4⇒4^x=8 1/4⇒x=log(4)33-1
a2=3⇒log(2)(4^x-8)=3⇒4^x-8=8⇒4^x=16⇒x=2
Ответ дал:
0
решение смотри во вложении
Приложения:
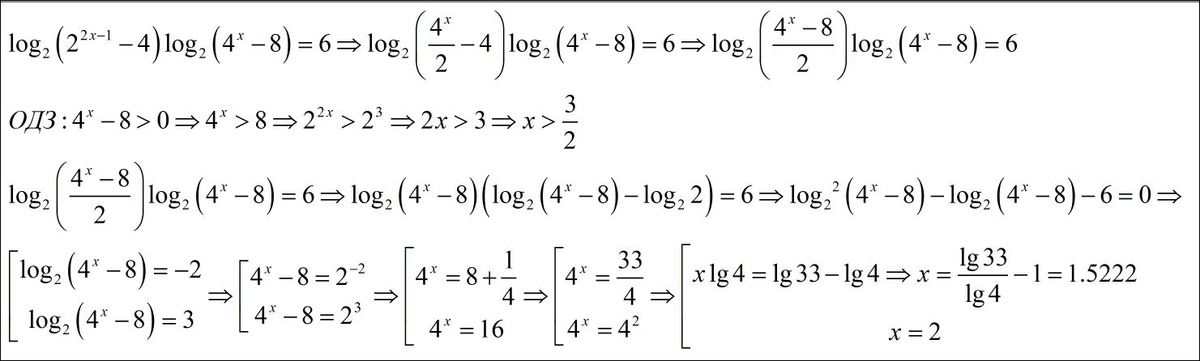
Похожие вопросы
2 года назад
7 лет назад
9 лет назад
10 лет назад