1 задача. Конец А отрезка АВ лежит в плоскости альфа. Через конец В и точку С этого отрезка проведены параллельные прямые, которые пересекают плоскость альфа соответственно в точке В1 и С1. Найти длину отрезка СС1, если ВВ1=16см и АС:ВС=3:5. 2 задача. Из точки, отстоящей от плоскости на расстоянии 12см, проведены две наклонные, образующие с плоскостью углы 45градусов и 60 градусов. Найти расстояние между основаниями наклонных, если угол между их проекциями прямой.
Ответы
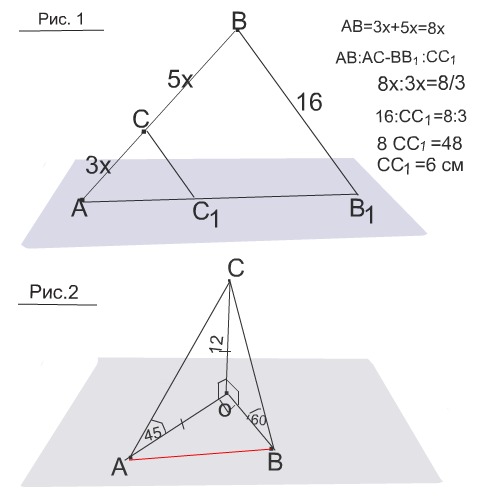
Решение первой задачи дано во вложенном рисунке
----
Решение задачи №2 (См.рисунок)
Проекция наклонной АС - это катет АО равнобедренного прямоугольного треугольника АОС, т.к. угол А=45°.
Проекция наклонной СВ - катет ОВ прямоугольного треугольника СОВ.
ОВ:СО=сtg (60°)
ОВ=СО·сtg (60°)
Ctg (60 градусов) = 1:√3
ОВ=12/√3
Преобразуем значение ОВ в более удобный вид, умножив числитель и знаменатель дроби на √3
ОВ=12√3):√3*√3=12√3):3=4√3
АВ=√(ОВ²+АО²)=√(48+144)=√192=8√3