• Предмет: Алгебра
  • Автор: Malkom
  • Вопрос задан 10 лет назад
< >

Найти площадь фигуры, огранниченной линиями y=2^x, y=4^x, x=1

Ответы

Ответ дал: midory
0

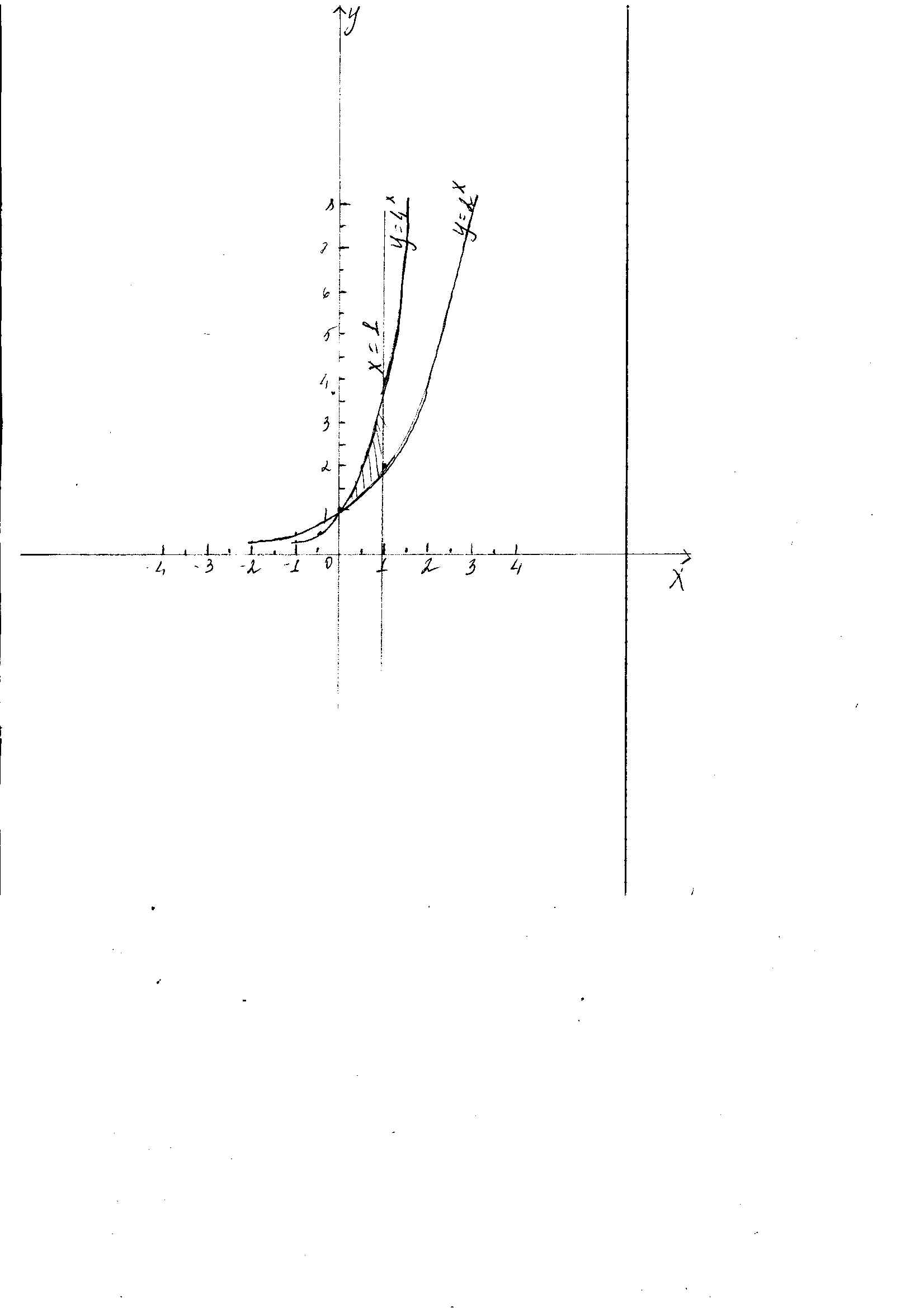
Как видно из рисунка который я приложила к решению нужно найти площадь заштрихованной фигуры. Площадь это интеграл, по х от 0 до 1 верхняя граница это 4^х нижняя - 2^x. То есть площадь выражается:S=intlimits^1_0 {4^{x}-2^{x}} , dx=intlimits^1_0 {4^{x}} , dx-intlimits^1_0 {2^{x}} , dx=\\ =frac{4^{x}}{ln4}|^1_0-frac{2^{x}}{ln2}|^1_0=frac{4^{1}}{ln4}-frac{4^{0}}{ln4}-frac{2^{1}}{ln2}+frac{2^{0}}{ln2}=frac{4}{2ln2}-frac{1}{2ln2}-frac{2}{ln2}+frac{1}{ln2}=\\ =frac{4-1-4+2}{2ln2}=frac{1}{2ln2}

Приложения:
Похожие вопросы
Русский язык
2 года назад
с указанными словами составьте такие пары словосочетаний или предложений, чтобы не надо было писать в одном случаи слитно, а в другом-раздельно. Образец: нелегкий путь (то есть тяжёлый) - не легкий,
Русский язык
2 года назад
Что такое взоры:).............
Химия
8 лет назад
120 г раствора содержится 3,6 г соли. Какова процентная концентрация раствора?
Химия
8 лет назад
Составьте уравнение реакции. CH4-CO2-C6H12O6-C6H5OH-C2H4-C2H5CL-C4H10
Математика
10 лет назад
Из 2-ух портов S между которыми 83 км.,одновременно в противоположных направлениях вышли 2 теплохода.Скорость 1-ого теплохода 32 км/ч.Через 4 часа S между ними было 335 км. Сколько км. проплыл 2-ой
Геометрия
10 лет назад
прямые a и b скрещивающиеся и прямые a и c скрещивающиеся. можно ли утверждать,что прямые b и c скрещивающиеся?
Математика
10 лет назад
расстояние от кончика носа ехидны до кончика ее хвоста 80 см длина мордочки 5см хвоста 1см какова длина телааааа ехидны
Математика
10 лет назад
две сестры и младший брат слепили 24 вареника.сестры слепили по 9 вареников.сколько вареников слепил брат?