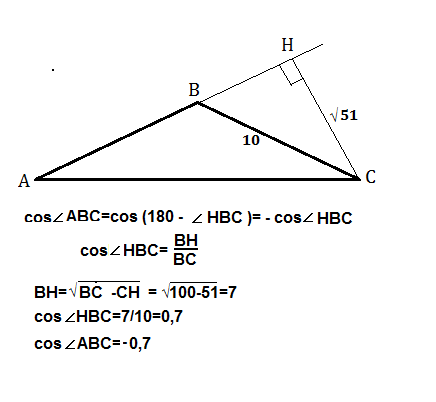
В тупоугольном треугольнике ABC AB=BC AB=10 высота CH равна корню из 51 Найдите косинус угла ABC по теореме Пифагора
Ответы
Ответ дал:
0
Высота тупоугольного треугольника, проведенная не из тупого угла, находится вне его плоскости и пересекает продолжение стороны, к которой проведена.
АВ=ВС, следовательно, основание АС.
Углы при основании равны. Поскольку в треугольнике не может быть два тупых угла. тупой угол - АВС.
Косинус тупого угла равен косинусу смежного с ним острого. взятому с обратным знаком.
сos ∠ABC=. - cos∠HBC=-HB/BC
HB=√(BC²-CH²)=√(100-51)= 7
сos ∠ABC=. - cos∠HBC=-7/10=-0,7
АВ=ВС, следовательно, основание АС.
Углы при основании равны. Поскольку в треугольнике не может быть два тупых угла. тупой угол - АВС.
Косинус тупого угла равен косинусу смежного с ним острого. взятому с обратным знаком.
сos ∠ABC=. - cos∠HBC=-HB/BC
HB=√(BC²-CH²)=√(100-51)= 7
сos ∠ABC=. - cos∠HBC=-7/10=-0,7
Приложения:
Похожие вопросы
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад
10 лет назад