Предмет: Геометрия
Автор: missyulya17
Вопрос задан 9 лет назад

< >

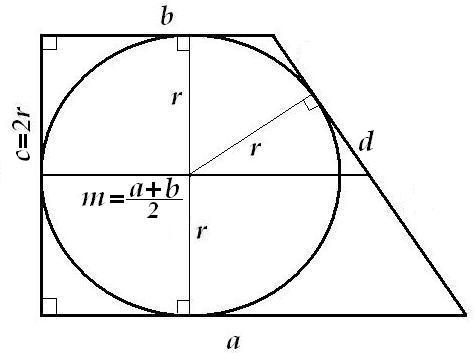
Докажите, что большая боковая сторона описанной прямоугольной трапеции равна удвоенной разнице средней линиии радиуса вписанной окружности.

Ответы

Ответ дал: okneret

0

Использовано свойство средней линии, свойство касательных, проведенных из однной точки к одной окружности

Приложения:

Ответ дал: missyulya17

0

Спасибо большое

Ответ дал: Аноним

0

Вспоминаем одно из общих свойств трапеции:
В трапецию можно вписать окружность только тогда, когда сумма длин оснований трапеции равна сумме длин её боковых сторон:
$a+b=c+d$
Смотрим картинго:
$a+b=2m\c=2r\2m=2r+d\d=2m-2r\d=2(m-r)$
ЧТД

Приложения:

Похожие вопросы

Геометрия

2 года назад

Высота прямоугольного треугольника делит прямой угол на 2 угла, один из которых на 30 гр меньше другого. Найдите острые углы данного треугольника. Помогите!!! У меня кр((

Русский язык

2 года назад

какое спряжение у слова понеслись?

Алгебра

7 лет назад

выбери точки которые лежат в 3 координатной четверти А(2;-5); В(-2;5); С(2;5) к(-2;-5)

Физика

7 лет назад

Як рухається тіло, якщо сума всіх сил, прикладених до нього, дорівнює нулю? *

Математика

9 лет назад

длина прямоугольного параллепипида 14 см . ширина состовляет 3/7 длины , а высота 0 , 8 ширины . найдите площадь основания и обьем параллепипида

Алгебра

9 лет назад

Помогите, пожалуйста, решить систему

Литература

10 лет назад

Класс 8,предмет литература,помогите пжл,кто читал "Мцыри",сочинение по нему надо написать:(

Физика

10 лет назад

1.как изменится период колебаний качелей,если на них вместо одного человека сядут двое? 2.как изменится период колебаний качелей,если,сидящий на них человек, встанет на сиденье? 3.как изменится