Даю 40 баллов.


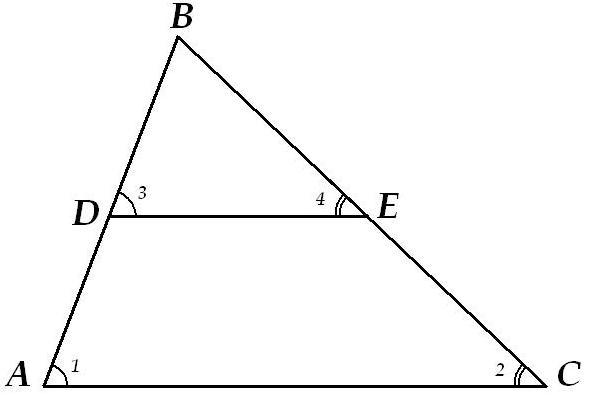
Дан треугольник АВС. ДЕ - параллелен к стороне АС (Д лежит на стороне АВ. Е - на стороне ВС). АВ=15 АС=18 АД=7,5. Найдите ДЕ.

Тема:Схожесть треугольников.
Прошу подробное объяснение.

∠1=∠3, ∠2=∠4 (как соответственные углы при пересечении параллельных прямых секущей), ∠В - общий угол, значит ΔАВС~ΔDBE по третьему признаку подобия треугольников.
DB=AB-AD=15-7,5=7,5 cм
Далее по подобию треугольников:



 см

Так решается, поскольку нужно решить с применением темы подобие треугольников. Можно и проще:
Если AD=DB=7,5 cм и DE || AC, то DE - средняя линия ΔАВС и равна:
 см