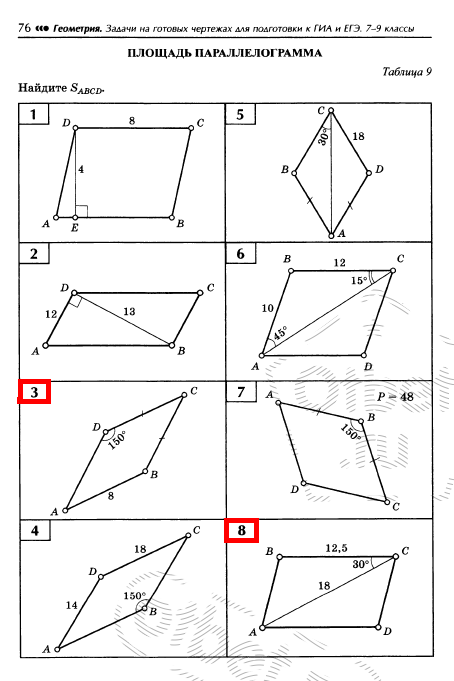
Помогите решить геометрию, пожалуйста. Очень плохо в ней разбираюсь. Даже в таких элементарных заданиях (выделенные номера: 3,8)

У параллелограмма противоположные стороны и углы равны.
Диагональ параллелограмма делит его на два равных треугольника.
Запомним эти свойства и воспользуемся ими.

3)
Дано:



Требуется найти площадь параллелограмма  

Следуя условию и свойству параллелограмма, имеем:



Но:

Следовательно, все стороны равны и наш параллелограмм является Ромбом.
Отсюда площадь, через угол и сторону:
- где а это сторона, альфа угол.
- см^2

8)
Используя свойство диагонали параллелограмма, мы получаем следующее:


Отсюда формула площади:
- где  площадь треугольника.

Находим площадь треугольника через стороны и угол между ними:
см^2

В итоге:
- см^2