В прямоугольной трапеции АВСД( угол ВАД=90) с основанием АД=24 и ВС=16 диагонали пересекаются в точке М, АВ=10
А) докажите, что треугольники ВМС и АМД подобны
Б) найти площадь треугольника АМД

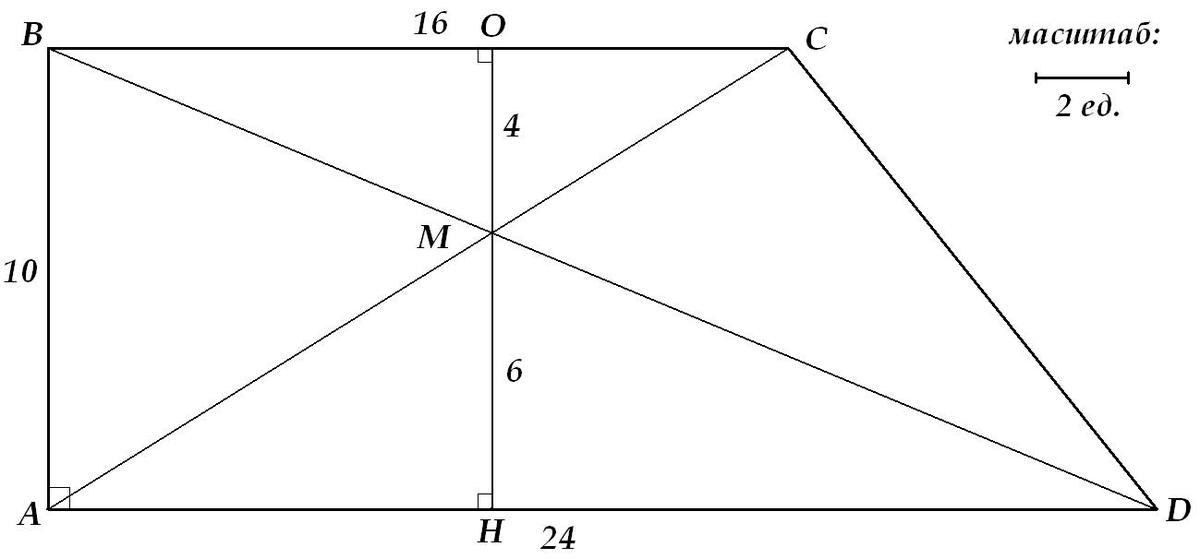
Смотрим картинго (пропорци, между прочим, соблюдены):
Вспоминаем чудесное правило:
При пересесечении диагоналей трапеции, треугольники, лежащие на основаниях подобны. Доказывется это легко, через равенство двух пар накрест лежащих и одной пары вертикальных углов.
ΔAMD~ΔCMB, MH и МО - высоты ΔAMD и ΔCMB, соответственно. Значит



Если кто-то готов с этим поспорить ну давайте, дерзните...







Всё...