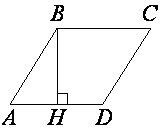
1)Высота BH ромба ABCD делит его сторону AD на отрезки AH=11 и HD=50. Найдите площадь ромба.

Все стороны ромба равны, поэтому
АD = AB = BC = CD = AH + HD = 11 + 50 = 61

По условию ВН – высота ромба

Рассмотрим ∆ ВАН (угол АНВ = 90°):
По теореме Пифагора:
АВ² = ВН² + АН²
ВН² = АВ² - АН²
ВН² = 61² - 11² = 3721 - 121 = 3600

Значит, ВН = 60

Площадь ромба рассчитывается по формуле параллелограмма:

S = a × h = AD × BH = 61 × 60 = 3660


ОТВЕТ: 3660