Предмет: Геометрия
Автор: Мимолетная
Вопрос задан 9 лет назад

Помогите пожалуйста, сравнивать буквы не надо)
очень прошу, пожалуйста
если в варианте №5, во втором задании ответ получится а-в, то решение не нужно)

Приложения:

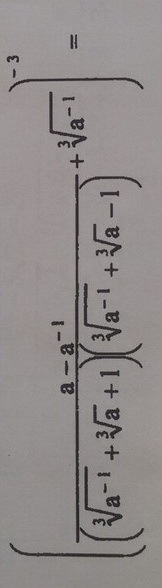
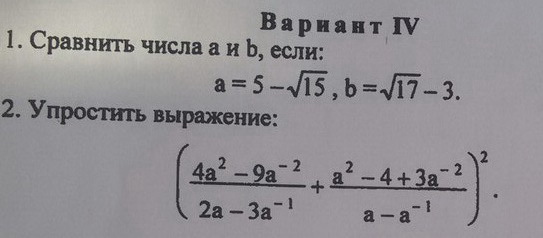
Ответы

Ответ дал: NNNLLL54

$1); ...=left ( frac{a-a^{-1}}{((a^{-frac{1}{3}}+a^{frac{1}{3}})+1)((a^{-frac{1}{3}}+a^{frac{1}{3}})-1)} +a^{-frac{1}{3}}right )^{-3}=\\=left ( frac{a-a^{-1}+a^{-frac{1}{3}}cdot ((a^{-frac{1}{3}}+a^{frac{1}{3}})^2-1)}{(a^{-frac{1}{3}}+a^{frac{1}{3}})^2-1}right )^{-3}=left ( frac{a-a^{-1}+a^{-frac{1}{3}}cdot (a^{-frac{2}{3}}+1+a^{frac{2}{3}})}{a^{-frac{2}{3}}+2+a^{frac{2}{3}}-1} right )^{-3}=$

$= frac{(a^{-frac{2}{3}}+1+a^{frac{2}{3}})^3}{(a-a^{-1}+a^{-1}+a^{frac{1}{3}}+a^{-frac{1}{3}})^3} = frac{(a^{-frac{2}{3}}+1+a^{frac{2}{3}})^3}{(a^{frac{1}{3}}cdot (a^{frac{2}{3}}+1+a^{-frac{2}{3}}))^3} =frac{1}{a}; ;$

$2); ...=left ( frac{4a^2-frac{9}{a^2}}{2a-frac{3}{a}} + frac{a^2-4+frac{3}{a^2}}{a-frac{1}{a}} right )^2=left ( frac{(4a^4-9)cdot a}{(2a^2-3)cdot a^2} + frac{(a^4-4a^2+3)cdot a}{(a^2-1)cdot a^2} right )^2=\\=left ( frac{(2a^2-3)(2a^2+3)}{(2a^2-3)cdot a} + frac{(a^2-1)(a^2-3)}{(a^2-1)cdot a} right )^2=left ( frac{(2a^2+3)+(a^2-3)}{a} right )^2=\\=left (frac{3a^2}{a}right )^2=(3a)^2=9a^2$

$3)left ( frac{1}{(a+b)^{-2}} - left (frac{a-b}{a^3+b^3} right )^{-1}right )cdot (ab)^{-1}=left ( (a+b)^2-frac{(a+b)(a^2-ab+b^2)}{a-b} right )cdot frac{1}{ab} \\= frac{(a+b)^2(a-b)-(a+b)(a^2-ab+b^2)}{(a-b)cdot ab} = frac{(a+b)((a+b)(a-b)-a^2+ab-b^2)}{(a-b)cdot ab} = \\=frac{(a+b)(a^2-b^2-a^2+ab-b^2)}{(a-b)cdot ab} = frac{(a+b)cdot b(a-2b)}{(a-b)cdot ab} =frac{(a+b)(a-2b)}{a(a-b)}\$

Похожие вопросы

География

2 года назад

самый большой океан на планете

Математика

2 года назад

основанием коробки является квадратом со сторонами 8 см. а высота равна 1 дм.

Химия

7 лет назад

Складіть рівняння реакції за наведеними схемами:P+O2---->P2O

Алгебра

7 лет назад