(1+корень из 3i)^3=?
(1+корнеь из 3I) ^5 =?
(1+i)^-3степени=?
(1+i)в минус6 стпени =?
Вычислите и изобразите на комплексной плоскости
3^корень 64
3^корень из -27
Ответы
Ответ дал:
0
Рассмотрим  . Модуль комплексного числа
. Модуль комплексного числа  . Тогда
. Тогда

Согласно формуле Муавра:

Аналогично делаем и со вторым примером(По формуле Муавра).

Рассмотрим . Тогда
. Тогда  и
и 
По формуле Муавра:
![boxed{z^{-3}=( sqrt{2} )^{-3}bigg[cosbigg(-dfrac{3pi}{4} bigg)+isinbigg(-dfrac{3pi}{4} bigg)bigg]= - frac{1}{4} - frac{i}{4} } boxed{z^{-3}=( sqrt{2} )^{-3}bigg[cosbigg(-dfrac{3pi}{4} bigg)+isinbigg(-dfrac{3pi}{4} bigg)bigg]= - frac{1}{4} - frac{i}{4} }](https://tex.z-dn.net/?f=boxed%7Bz%5E%7B-3%7D%3D%28+sqrt%7B2%7D+%29%5E%7B-3%7Dbigg%5Bcosbigg%28-dfrac%7B3pi%7D%7B4%7D+bigg%29%2Bisinbigg%28-dfrac%7B3pi%7D%7B4%7D+bigg%29bigg%5D%3D+-+frac%7B1%7D%7B4%7D+-+frac%7Bi%7D%7B4%7D+%7D)
Аналогично
![boxed{z^{-6}=( sqrt{2} )^{-6}bigg[cosbigg(-dfrac{6pi}{4} bigg)+isinbigg(-dfrac{6pi}{4} bigg)bigg]= frac{i}{8} } boxed{z^{-6}=( sqrt{2} )^{-6}bigg[cosbigg(-dfrac{6pi}{4} bigg)+isinbigg(-dfrac{6pi}{4} bigg)bigg]= frac{i}{8} }](https://tex.z-dn.net/?f=boxed%7Bz%5E%7B-6%7D%3D%28+sqrt%7B2%7D+%29%5E%7B-6%7Dbigg%5Bcosbigg%28-dfrac%7B6pi%7D%7B4%7D+bigg%29%2Bisinbigg%28-dfrac%7B6pi%7D%7B4%7D+bigg%29bigg%5D%3D+frac%7Bi%7D%7B8%7D+%7D)
![sqrt[3]{64} sqrt[3]{64}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B64%7D+)
Рассмотрим . Тогда
. Тогда 
По формуле Муавра:
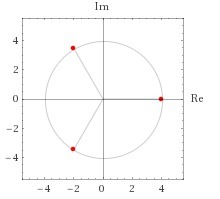
![boxed{ sqrt[3]{z}=4bigg(cos frac{2 pi k}{3}+isin frac{2 pi k}{3} bigg),~~~ k=0,1,2 } boxed{ sqrt[3]{z}=4bigg(cos frac{2 pi k}{3}+isin frac{2 pi k}{3} bigg),~~~ k=0,1,2 }](https://tex.z-dn.net/?f=boxed%7B+sqrt%5B3%5D%7Bz%7D%3D4bigg%28cos+frac%7B2+pi+k%7D%7B3%7D%2Bisin+frac%7B2+pi+k%7D%7B3%7D+bigg%29%2C%7E%7E%7E+k%3D0%2C1%2C2++%7D)
![sqrt[3]{-27} sqrt[3]{-27}](https://tex.z-dn.net/?f=+sqrt%5B3%5D%7B-27%7D+)
Рассмотрим
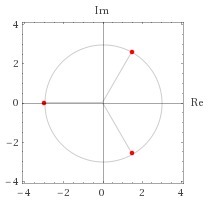
![boxed{ sqrt[3]{z}=3bigg(cos frac{ pi +2 pi k}{3}+isin frac{ pi +2 pi k}{3} bigg),~~~ k=0,1,2 } boxed{ sqrt[3]{z}=3bigg(cos frac{ pi +2 pi k}{3}+isin frac{ pi +2 pi k}{3} bigg),~~~ k=0,1,2 }](https://tex.z-dn.net/?f=boxed%7B+sqrt%5B3%5D%7Bz%7D%3D3bigg%28cos+frac%7B+pi+%2B2+pi+k%7D%7B3%7D%2Bisin+frac%7B+pi+%2B2+pi+k%7D%7B3%7D+bigg%29%2C%7E%7E%7E+k%3D0%2C1%2C2++%7D)
Согласно формуле Муавра:
Аналогично делаем и со вторым примером(По формуле Муавра).
Рассмотрим
По формуле Муавра:
Аналогично
Рассмотрим
По формуле Муавра:
Рассмотрим
Приложения:
Похожие вопросы
2 года назад
7 лет назад
10 лет назад
10 лет назад
10 лет назад