решите уравнение: 2 + cosx = 2tgx/2

Ответы

Ответ дал: antonovm

Решение : /////////////////////////////////////////

Приложения:

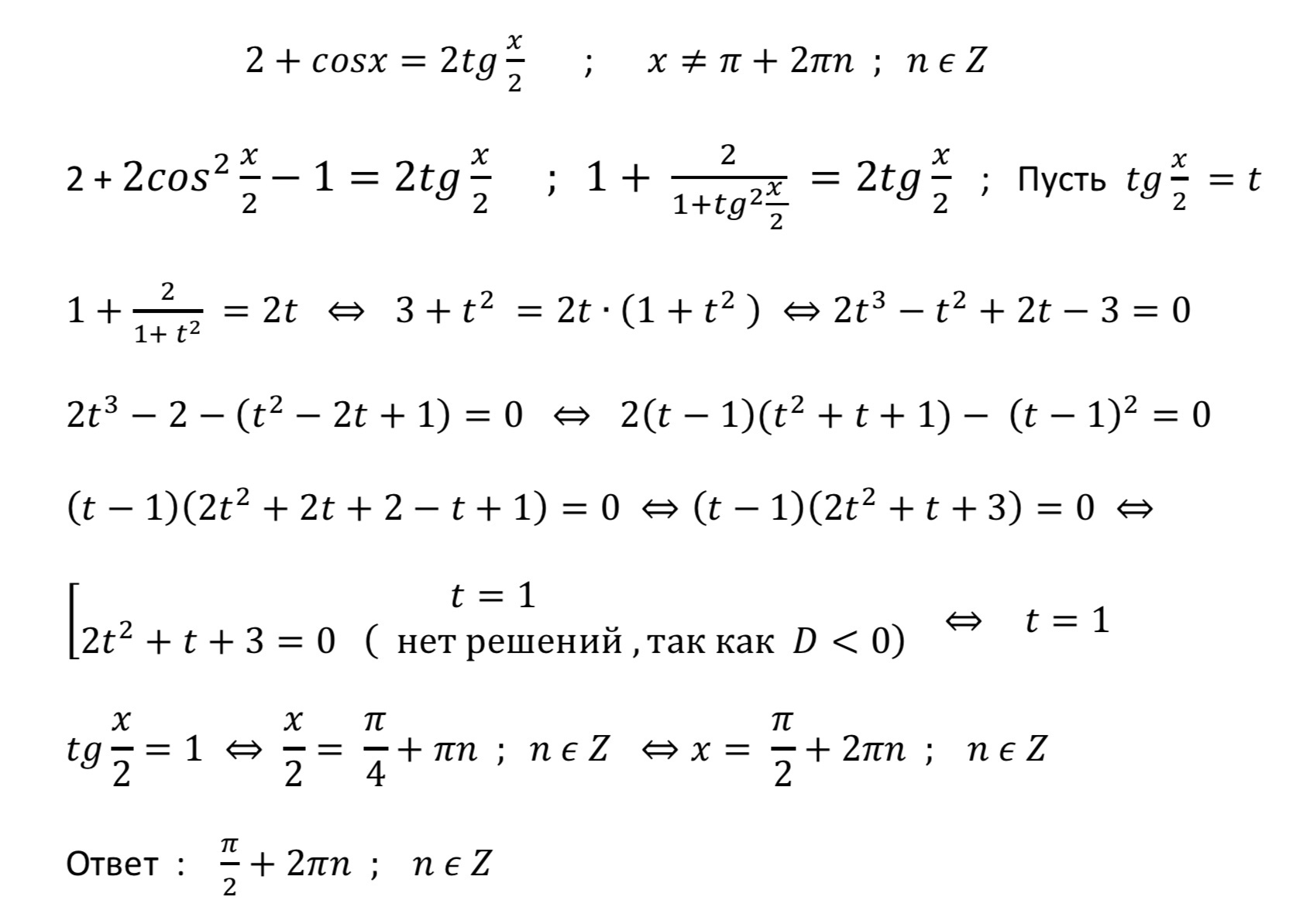
Ответ дал: as11111

Выразим косинус через тангенс половинного угла:

$2-2tg(frac{x}{2})+frac{1-tg^2(frac{x}{2})}{1+tg^2(frac{x}{2})}=0\(1-tg(frac{x}{2}))(2+frac{1+tg(frac{x}{2})}{1+tg^2(frac{x}{2})})=0\(1-tg(frac{x}{2}))(frac{2tg^2(frac{x}{2})+tg(frac{x}{2})+3}{1+tg^2(frac{x}{2})})=0$

У второй скобки решений нет, т.к. дискриминант квадратного трехчлена в числителе D = -23 < 0, а у первой скобки:

$tg(frac{x}{2})=1\frac{x}{2}=frac{pi}{4}+pi*n, nin Z\x=frac{pi}{2}+2pi*n, nin Z$

Приложения:

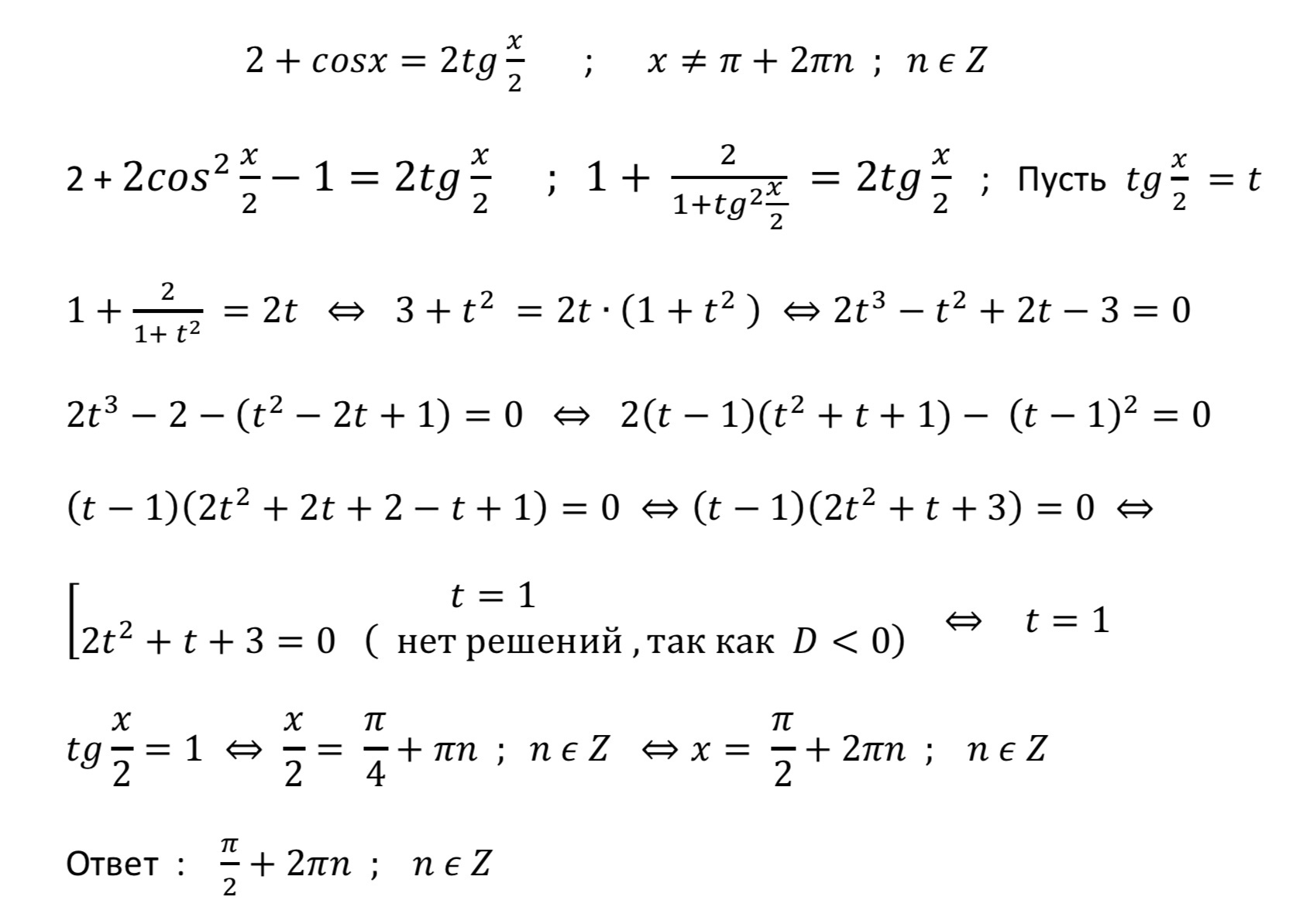
Похожие вопросы

Английский язык

2 года назад

№5 Выберите правильный вариант/ Укажите грамматическое время, которое вы выберите (Present Simple, Present Continuous, Present Perfect, Present Perfect Continuous; Past Simple, Past Continuous, Past

Другие предметы

2 года назад

Почему все религии Китая связаны с природой?

Геометрия

7 лет назад

1.Диоганали прямоугольника ABCD пересекаются в точке O,угол ABO равен 38°. найти угол AOD.

Математика

7 лет назад

СРОЧНО! Розбий частки на дві групи. Знайди значення часток. 760/20 720/80 960/80 960/30

История

10 лет назад

ПОЖАЛУЙСТА!!! Для русской культуры 10-13 вв. характерно единение в многообразии. Докажите это.

Математика

10 лет назад

бабушка подала к обеду 6 пирожков. сколько всего пирожков испекла бабушка если у неё осталось столько же и ещё полстолько?решение подробно

Химия

10 лет назад

Сплав магния и алюминия массой 75 г растворили в серной кислоте получив смесь сульфатов металлов массой 441 г.Какую массу магния надо сплавить с алюминием массой 540 г для получения такого сплава

Химия

10 лет назад

Для нейтрализации предельной одноосновной карбоновой кислоты массой 13,8г потребовалось 120г 10%-ного растовора гидроксида натрия. Определите формулу кислоты.