Предмет: Алгебра
Автор: anakonda1223
Вопрос задан 9 лет назад

Доказать равенство: Желательно поэтапно.
$sqrt{23-4 sqrt{15} } = 2 sqrt{5} - sqrt{3}$

Ответы

Ответ дал: v4volande

$sqrt{23-4sqrt{15}}=2sqrt{5}-sqrt{3}\$
Возведем левую и правую часть в квадрат
$23-4sqrt{15}=(2sqrt{5}-sqrt{3})^2\ 23-4sqrt{15}=20-4sqrt{5}sqrt{3}+3\ 23-4sqrt{15}=23-4sqrt{5*3}\ 23-4sqrt{15}=23-4sqrt{15}$

Ответ дал: anakonda1223

Спасибо! Теперь знаю, как доказывать подобные равенства.

Ответ дал: v4volande

Пожалуйста) Успехов в учёбе!

Ответ дал: owlefo

Смотри решение во вложении:

Приложения:

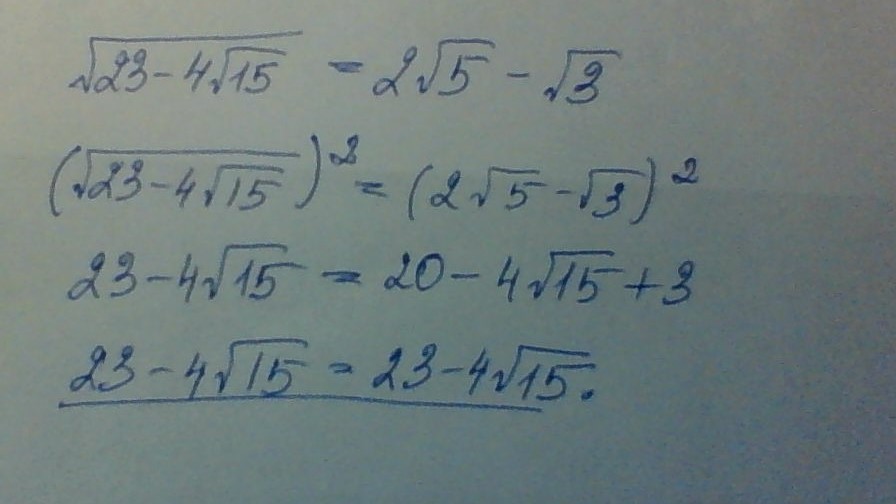
Похожие вопросы

История

2 года назад

Из донесений резидента «Рамзая»: «15 мая (1941 г.). «Война начнется 20-22 июня…Рамзай».«19 мая (1941 г.). «Против Советского Союза будет сосредоточено 9 армий, 150 дивизий…Рамзай». Какой известный

Русский язык

2 года назад

Написать звуко - буквенный анализ слова - ожил (полный фонетический разбор ) ЗАДАНИЕ ОТ САЙТА.

Физика

7 лет назад

Два одинаковые шарика имели заряды -9,3нКл и1,3нКл. Шарики привели в столкновение и раздвинули на 2 см. С какой силой они взаимодействуют? Какое число электронов на каждоми шарики после столкновения?

Алгебра

7 лет назад

решите систему уравнения методом сложения { 3х+8у=2 { 5х+4у=-20

Литература

9 лет назад

Сочинение лекго!!!!!!!!! Сделать сочинение про игрушку. Название игрушки - Машинка на пульте управление "План" 1. Где купили?,или как нашел,может подарили - ( 5,6,7,8- предложений l Желательно 8

Математика

9 лет назад

помогите плиз !задача 4 класса . Подъем на гору на фуникулере занимает 9 мин . Спуск на лыжах - 2 мин.На сколько выше скорость спуска ,если длина горнолыжной трассы 1530м?

Математика

10 лет назад

Для перевозки груза надо 20 автомобилей грузоподъемностью 6т. Сколько потребуется автомобилей грузоподъемностью 8т, чтобы перевести этот же груз? помогите плиз решить

Математика

10 лет назад

незнайка стал догонять шпунтика ,когда ростаяние между ними было равно 1 км 80 м. незнайка бежал со скоростью 170 м/мин ,а шпунтик шел со скоростью 80 м/мин .через сколько минут незнайка догонит