Кто силен в пределах помогите решить 2 вариант 3 пример(40 баллов)Помогите пожалуйста!
Приложения:
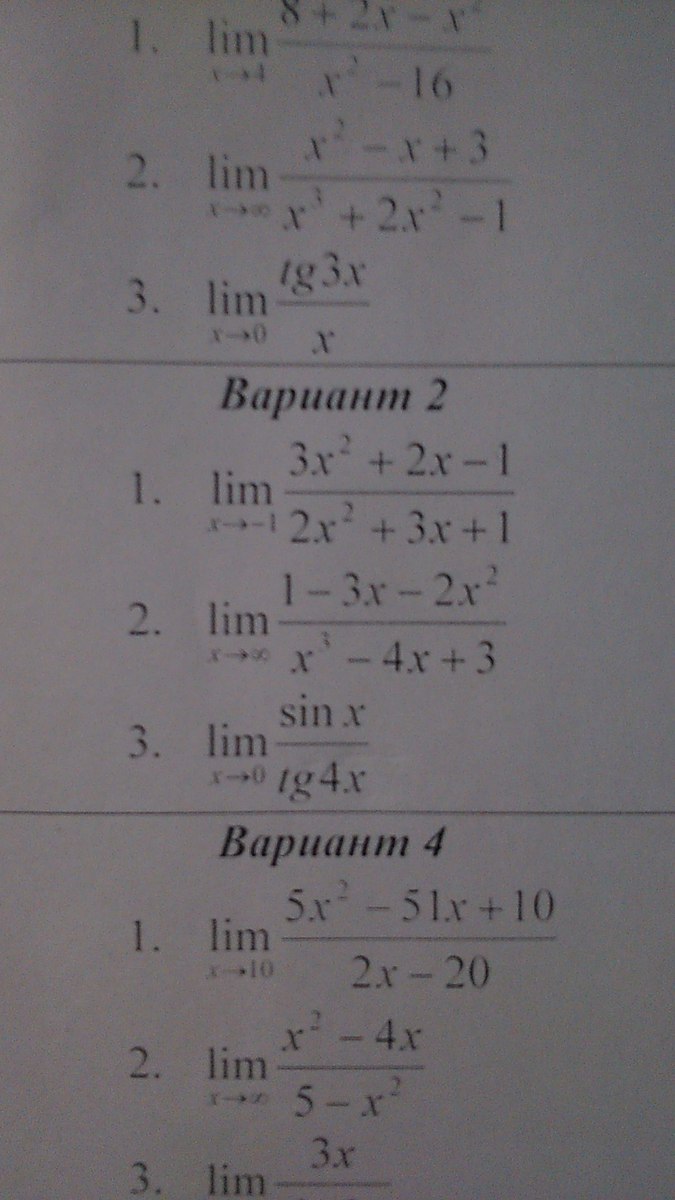
Ответы
Ответ дал:
0
Ответ дал:
0
...*1/4 = 1/4.
Ответ дал:
0
Ой, спасибо...
Ответ дал:
0
1) Limx→-1 (3x² +2x-1)/(2x² +3x+1) ||неопределенность типа 0/0 ||
= Limx→-1 (3x -1)(x+1) /(x+1)(2x+1) =Limx→-1 (3x -1) /(2x+1) =
(3*(-1) -1)/(2*(-1) +1) = (-4)/(-1) =4.
* * * 3x² +2x-1 =0 ⇒x₁= -1; x₂ =1/3. 3x² +2x-1=3(x+1)(x-1/3) =(x+1)(3x-2x² 2x²+3x+1 =0⇒x₁= -1; x₂ =1/2. 2x²+3x+1 =2(x+1)(x+1/2) =(x+1)(2x+1)
Второй корень можно было определить по теорему Виета * * *
-------
2) Limx→∞ (1-3x-2x²)/(x³-4x+1) =Limx→∞ (1/x³ -3/x² -2/x)/(1-4/x² +1/x³) =0.
* * *(0-0 -0)/(1 -0 -0) =0/1 =0 * * *
-------
3) Limx→0 sinx/tq4x = Limx→0 (1/4)*( (sinx)/x)) / ((tq4x) /4x)) =
(1/4)*( Limx→0 (sinx)/x) ) / ( Limx→0 (tq4x)/4x)) =(1/4)* (1/1) =4 .
= Limx→-1 (3x -1)(x+1) /(x+1)(2x+1) =Limx→-1 (3x -1) /(2x+1) =
(3*(-1) -1)/(2*(-1) +1) = (-4)/(-1) =4.
* * * 3x² +2x-1 =0 ⇒x₁= -1; x₂ =1/3. 3x² +2x-1=3(x+1)(x-1/3) =(x+1)(3x-2x² 2x²+3x+1 =0⇒x₁= -1; x₂ =1/2. 2x²+3x+1 =2(x+1)(x+1/2) =(x+1)(2x+1)
Второй корень можно было определить по теорему Виета * * *
-------
2) Limx→∞ (1-3x-2x²)/(x³-4x+1) =Limx→∞ (1/x³ -3/x² -2/x)/(1-4/x² +1/x³) =0.
* * *(0-0 -0)/(1 -0 -0) =0/1 =0 * * *
-------
3) Limx→0 sinx/tq4x = Limx→0 (1/4)*( (sinx)/x)) / ((tq4x) /4x)) =
(1/4)*( Limx→0 (sinx)/x) ) / ( Limx→0 (tq4x)/4x)) =(1/4)* (1/1) =4 .
Ответ дал:
0
нужно было только 3,но спасибо большое
Похожие вопросы
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад