Школьник решил прокатиться в метро одного из городов. Понаблюдав за поездами, он понял, что интервал их движения составляет T=1 мин 40 c, при этом все поезда стоят на станции в течение Δt=30 c. Определите дистанцию между поездом в момент его отправления со станции и позади идущим составом. Длина каждого поезда составляет L=100 м. Ответ выразите в мм, округлив до целых. Под дистанцией подразумевается расстояние между хвостом впереди идущего поезда и головой позади идущего. Известно, что до отправления поезда со станции позади идущий состав успевает разогнаться до постоянной скорости V.

В задаче не сказано, как именно останавливается поезд.

Можно было бы предположить, что поезда останавливаются мгновенно, как в примитивной компьютерной игре, однако, читая последнее предложения, мы понимаем, что рассматривается более-менее реальная ситуация, где поездам нужно время для того, чтобы разгоняться, а значит и останавливаться.

[[ I ]] Если предположить, что в задаче должен быть указан период и время торможения, то тогда в ней должны использоваться два дополнительных параметра: – время и – период торможения.

[[ II ]] Если же предположить, что поезда останавливаются с постоянным ускорением то решение будет содержать этот дополнительный параметр.



Решим задачу для обоих вариантов восстановленного условия:



[[ I ]]

Дано в конкретных з н а ч е н и я х :

Интервал движения
Время посадки высадки
Длина состава м .

дано п а р а м е т р а м и :

Штатная скорость ;
Время торможения до остановки ;
Тормозной путь ;


Найти: дистанцию между составами .




Р е ш е н и е :


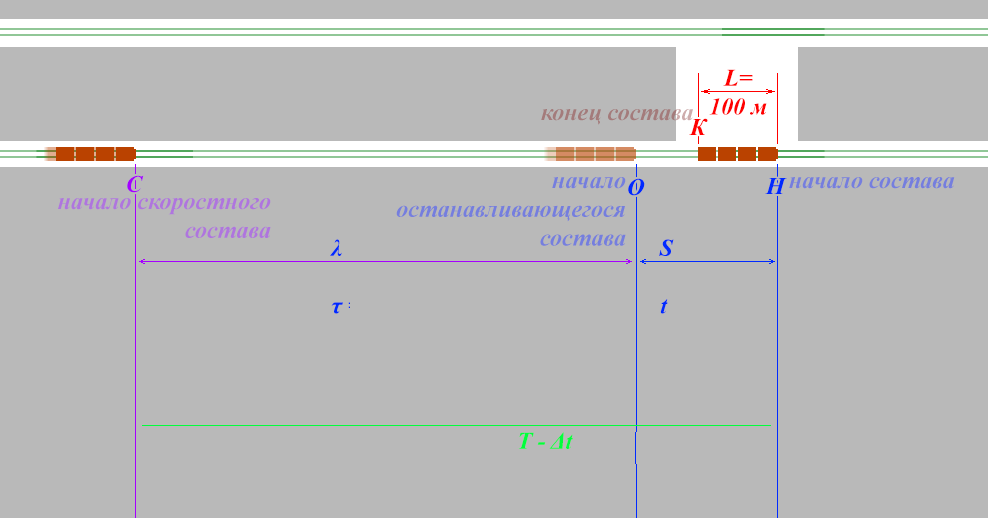
Все положения, упоминаемые в доказательстве решения, отмечены на приложенном к решению рисунке.

Искомая дистанция между поездами – это свободное пространство вдоль железнодорожного полотна. Таким образом – дистанция в данном случае – это расстояние от ведущего вагона (начала) заднего Скоростного состава (положение С) до Конца припаркованного состава (положение К) в тот момент, когда припаркованный собирается отправляться.

Нам неизвестно, является ли торможение составов перед остановкой равнозамедленным или нет, и нам это знать и не нужно (!), поскольку нам дано и время, и скорость, и тормозной путь. Всё, что нам нужно – это корректно учесть все слагаемые времени и пути при торможении.

Общий интервал движения составляет и это означает, что каждые секунд, в положении Н оказывается Начало очередного состава. Уже припаркованный состав простоял на станции а это означает, что следующему за ним составу осталось проехать из положения С (начало скоростного состава) до точки Н (начало припаркованного состава) в течение секунд.

Искомая дистанция между составами, как мы уже говорили выше, измеряется не от положения С до положения Н, а от положения С до положения К (конец припаркованного состава). Однако нам будет удобно найти весь остаточный путь СН (между положениями С и Н), а затем вычесть из него длину КН (между положениями К и Н), равную длине состава м.

Из секунд, оставшихся идущему следом составу, первые секунд он будет идти с постоянной скоростью из положения С в положение О, а последующие секунд он будет останавливаться из положения О до положения Н.

Длину отрезка ОН – это тормозной путь . Теперь найдём СО, т.е. длину Мы знаем, что по отрезку СО состав двигается равномерно со скоростью в течение времени значит отрезок СО, т.е.

Отсюда ясно, что вся длина СН = СО + ОН , т.е.
СН

Как было показано выше искомая дистанция – это длина СК, равная разности СН и КН, т.е. СН и .

Итак: СК CH

м м .



О т в е т [[ I ]] :

дистанция между составами в аналитической форме

;

дистанция между составами с подстановкой известных величин:

м ,

где – штатаная скорость состава,
– время торможения, и – тормозной путь.




*** [[ II ]] Решение задачи для второго варианта восстановленного условия во вложенной картинке:

О т в е т [[ II ]] :

дистанция между составами в аналитической форме

;

дистанция между составами с подстановкой известных величин:

м ,

где – штатаная скорость состава,
и – модуль ускорения при торможении.

спасиб

ОТВЕТ 100???

КАКОЙ ТОЧНЫЙ

Ответ дан формулой, для всех таких задач. В формулу (лучше всего из ответа [[[1]]] ) нужно подставить конкретные знаения для V, t и S. Так если, например: V = 57.6 км/ч = 16 м/с, t = 20 c и S = 160 м., то тогда ::: D = 16 ( 70 c - 20 с ) + 160 м - 100 м = 16 * 50 c + 60 м = 860 м.

При других данных и другой численный ответ. Но формула в ответе используется всегда одна и та же.