Выполнить исследование функции по следующей схеме:
1)найти область определения
2)проверить четность-нечетность функций
3)найти точки пересечения с осями координат
4)найти экстремумы и интервалы монотонности
5)найти точки перегиба и интервалы выпуклости и вогнутости
6)найти пределы функций при x (+)(-)бесконечности
7)построить график функции.

y=3x^3-15x^2+36x-5 ``Пожалуйста``

1) Область определения: x ∈ (-∞; ∞).
2) Четность-нечетность:



Т.к.  и , то функция является функцией общего вида.
3) Точки пересечения с Ox. Решим исходное уравнение при y = 0. (метод решения: Виета-Кардано)
Получим один корень: x = 0.148 - абсцисса точки пересечения графка с осью Ox. Координаты точки: (0.148; 0)

Точка пересечения с Oy. Найдем y, подставив в уравнение x = 0. Получим: y = -5. Координаты точки: (0, -5).

4) Так как функция кубическая, то точек экстремума не имеет.

5) Первая производная.


2. Вторая производная.

Находим корни уравнения. Для этого полученную функцию приравняем к нулю.

Откуда точка перегиба:
x = 5/3

На промежутке: (-∞ ;5/3)

Значит, функция выпукла.

На промежутке (5/3; ∞)

Значит, функция вогнута. 

6) 


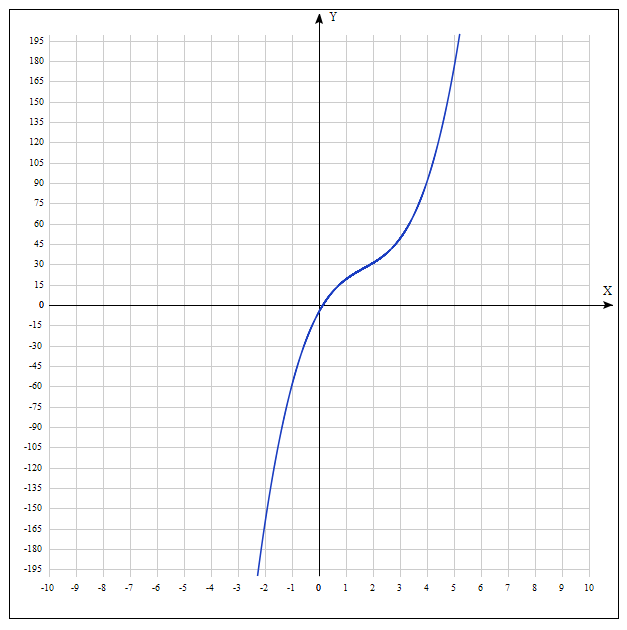
7(график в приложениях)

Как мог.. Работа объемная, конечно)